MrShoe
- 3
- 0
Hello everyone,
Being new here, and not a "Physics Guy" I wasn't sure where this should go, but General Physics seemed like the best bet.
Recently I've been thinking about the effects of circular motion on external objects, and I've hit dead end with one of my trains of thought.
Excuse the crude drawing, but this is what I'm looking at:
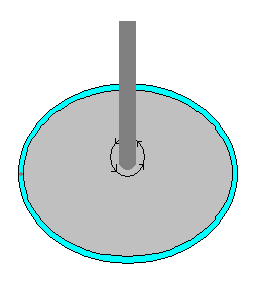
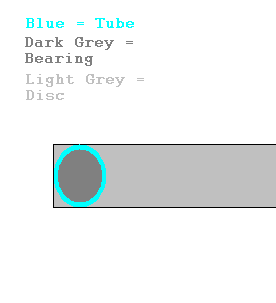
The above picture shows a round disc (meant to be perfectly round/balanced) attached to a drive shaft, with a blue ring on the outside containing a ball bearing. The ring would be a tube inside the outer perimeter of the disc (see below image):
As the disc starts to spin, I imagine that the bearing would also move, probably spinning in the opposite direction, but moving in the same direction. What I'd like to figure out is at what RPM would the bearing stop moving completely, and the factors that can and will change this.
For simplicity, let's say the disc has a diameter of 4" and the ball bearing has a mass of 0.5g. The drive shaft can spin from 0-600 RPM.
I'm sorry if this is vague, I tried to word it the best way I could. If anymore information is needed please let me know.
Thank you!
Being new here, and not a "Physics Guy" I wasn't sure where this should go, but General Physics seemed like the best bet.
Recently I've been thinking about the effects of circular motion on external objects, and I've hit dead end with one of my trains of thought.
Excuse the crude drawing, but this is what I'm looking at:
The above picture shows a round disc (meant to be perfectly round/balanced) attached to a drive shaft, with a blue ring on the outside containing a ball bearing. The ring would be a tube inside the outer perimeter of the disc (see below image):
As the disc starts to spin, I imagine that the bearing would also move, probably spinning in the opposite direction, but moving in the same direction. What I'd like to figure out is at what RPM would the bearing stop moving completely, and the factors that can and will change this.
For simplicity, let's say the disc has a diameter of 4" and the ball bearing has a mass of 0.5g. The drive shaft can spin from 0-600 RPM.
I'm sorry if this is vague, I tried to word it the best way I could. If anymore information is needed please let me know.
Thank you!