yy205001
- 60
- 0
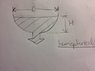
what is the cross section area of the water??
Determine an expression for the cross sectional area A of the fluid in the tank as a function of D and H.
A=pi*r2
i try to let the radius equal to the height but then the fluid's height goes lower, it doesn't form a circle anymore. So i have no ideas how to do this.Please help.
Homework Statement
Determine an expression for the cross sectional area A of the fluid in the tank as a function of D and H.
Homework Equations
A=pi*r2
The Attempt at a Solution
i try to let the radius equal to the height but then the fluid's height goes lower, it doesn't form a circle anymore. So i have no ideas how to do this.Please help.