DarkDrag0nite
- 15
- 0
This is not really the homework. It is the university examination problem. The problem here is many teachers/professors answer differently and not much detailed. And we don't know who was the exact professor who create these problems.
Instuction: Find the number of "Degree of Freedom (dof)" in the system.
First System
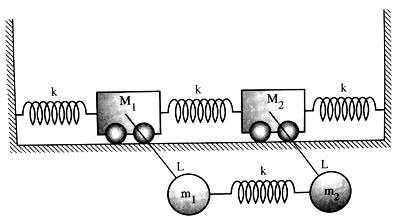
Second System
(Please ignore unreadable words, they're Thai language but you can understand by their variables)
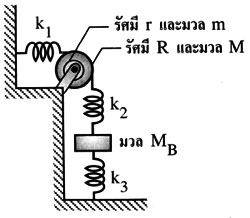
I don't think there is any relevant equation here.
For the First System:
Absolutely, 2 Boxes (M1 and M2) can move left and right. So there are 2 dof.
The 2 sphere (m1 and m2) with the rope can move in circular. So there are 2 dof.
I'm not sure if we also consider 2 sphere that they can move left and right or not ?
If we do, so 6 dof. If not, so 4 dof.
What's should I answer ? 6 or 4 dof ?
For the Second System:
There are two pulleys stuck together (m and M) so we consider as one object which can rotate in 1 circular direction. So there is 1 dof.
The box (MB) can move up and down. So there is 1 dof.
Here is problem, some professors said that the box can move in 3 axis which is 3 dof. Is it reasonable ?
I myself think the box should have only 1 dof which corresponds to the system.
Should answer to this system be 2 dof or 4 dof ?
Any help is appreciative. (I will be at school and not be able to reply for 2 days)
Homework Statement
Instuction: Find the number of "Degree of Freedom (dof)" in the system.
First System
Second System
(Please ignore unreadable words, they're Thai language but you can understand by their variables)
Homework Equations
I don't think there is any relevant equation here.
The Attempt at a Solution
For the First System:
Absolutely, 2 Boxes (M1 and M2) can move left and right. So there are 2 dof.
The 2 sphere (m1 and m2) with the rope can move in circular. So there are 2 dof.
I'm not sure if we also consider 2 sphere that they can move left and right or not ?
If we do, so 6 dof. If not, so 4 dof.
What's should I answer ? 6 or 4 dof ?
For the Second System:
There are two pulleys stuck together (m and M) so we consider as one object which can rotate in 1 circular direction. So there is 1 dof.
The box (MB) can move up and down. So there is 1 dof.
Here is problem, some professors said that the box can move in 3 axis which is 3 dof. Is it reasonable ?
I myself think the box should have only 1 dof which corresponds to the system.
Should answer to this system be 2 dof or 4 dof ?
Any help is appreciative. (I will be at school and not be able to reply for 2 days)