What is the Effect of Mass on Earth's Angular Velocity?

[temaire]

Homework Statement

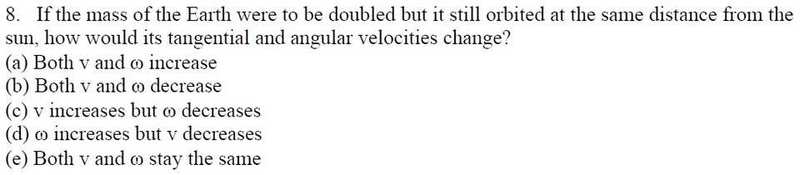
The attempt at a solution
I think the answer is (b) because an increase in mass would cause an increase in inertia of Earth. This would decrease the velocity of Earth, and since velocity is proportional to angular velocity, both would decrease. Am I right?

 

[ehild]

The Earth stays on the same orbit. Think of Kepler's third law about the relation between distance from Sun and orbital period.

ehild