What Is the Ground State Energy of a Particle in a Box?

[szamito]

[SOLVED] Find the ground state energy

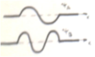
1. A particle is confined to a one dimensional box. Two possible state functions and the corresponding energies for the particles are shown in the figure. Find the ground state energy.

EA=4eV

EB=9eV

Homework Equations

E_n=(n^2 h)/(8mL^2 ); E_1=h/(8mL^2 ) then E_n=n^2 E_1

The Attempt at a Solution

E2 =4eV=22E1 then E1=1eV=1,6*10-19 J

 

[olgranpappy]

...

The Attempt at a Solution

E2 =4eV=22E1 then E1=1eV=1,6*10-19 J

okay, yes. And apparently by "22" you mean $2^2$.