rdg29
- 5
- 1
1. Problem statement:
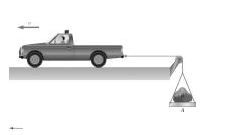
A 5000-lb truck is being used to lift a 1000-lb boulder B that is on a 200-lb pallet. Knowing the acceleration of the truck is 1 ft/s^2, determine the horizontal force between the tires and ground. The truck is on a horizontal plane with the boulder and pallet connected to a single pulley system off a cliff face.
∑F = ma
3. Attempt at the solution:
[STRIKE]Assuming no friction.
[/STRIKE]
First, I separated the truck and the boulder with two separate FBD/Kinematic diagrams.
For the truck, I had 4 total forces acting on the body.
F = ? (horizontal force between the truck and the ground)
T = ? (tension in the cable)
N = 5000 lb
W = -5000 lb
Setting up the sum of the forces on the truck, we get:
∑Fy = 0
∑Fx = F - T
(ma)sum = F - T
mtruck = 5000/32.2 = 155.280
Subbing in the known values:
155.280*1 ft/s^2 = F - T
Now, I moved to the pulley system:
The FBD consisted of 3 forces:
T = ? (tension in the cable)
Wb = Weight of the Boulder = 1000 lb
Wp = Weight of the Pallet = 200 lb
Setting up the sum of the forces, we get:
∑Fx = 0
∑Fy = T - Wb - Wp
Subbing in the known values:
mboulder+pallet = (1000 lb + 200 lb)/32.2 = 37.267
(mboulder+pallet*1 ft/s^2) = T - 1000-lb - 200-lb
T = 1237.267-lb
Use T to find F in the equation for the truck:
155.280 = F - 1237.267
F = 1392.5-lb
The problem I am running into however, is this does not match the answer I'm told to find. I'm wondering if it is just something simple that I'm missing here, so any guidance would be appreciated.
A 5000-lb truck is being used to lift a 1000-lb boulder B that is on a 200-lb pallet. Knowing the acceleration of the truck is 1 ft/s^2, determine the horizontal force between the tires and ground. The truck is on a horizontal plane with the boulder and pallet connected to a single pulley system off a cliff face.
Homework Equations
:[/B]∑F = ma
3. Attempt at the solution:
[STRIKE]Assuming no friction.
[/STRIKE]
First, I separated the truck and the boulder with two separate FBD/Kinematic diagrams.
For the truck, I had 4 total forces acting on the body.
F = ? (horizontal force between the truck and the ground)
T = ? (tension in the cable)
N = 5000 lb
W = -5000 lb
Setting up the sum of the forces on the truck, we get:
∑Fy = 0
∑Fx = F - T
(ma)sum = F - T
mtruck = 5000/32.2 = 155.280
Subbing in the known values:
155.280*1 ft/s^2 = F - T
Now, I moved to the pulley system:
The FBD consisted of 3 forces:
T = ? (tension in the cable)
Wb = Weight of the Boulder = 1000 lb
Wp = Weight of the Pallet = 200 lb
Setting up the sum of the forces, we get:
∑Fx = 0
∑Fy = T - Wb - Wp
Subbing in the known values:
mboulder+pallet = (1000 lb + 200 lb)/32.2 = 37.267
(mboulder+pallet*1 ft/s^2) = T - 1000-lb - 200-lb
T = 1237.267-lb
Use T to find F in the equation for the truck:
155.280 = F - 1237.267
F = 1392.5-lb
The problem I am running into however, is this does not match the answer I'm told to find. I'm wondering if it is just something simple that I'm missing here, so any guidance would be appreciated.
Last edited: