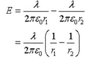What is the magnitude of the electric field (rod)?

In summary, the problem involves two uniformly charged thin glass rods placed side by side, each with a length of 11.3 cm and a separation distance of 4.70 cm. The question asks about the electric field along a line through the middle of the rods. Using the given values and relevant equations, the incorrect result of 1.21*10^5 N/C was obtained, possibly due to treating the rods as infinitely long. It is unclear if calculus is being used in the course, but it may be necessary to handle the case of finite length rods.
  • #1
sunnnystrong
54
6

Homework Statement


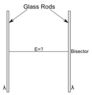
Two thin glass rods are placed side by side 4.70 cm apart as shown in the diagram below. They are each 11.3 cm long and are uniformly charged to +10.4 nC .

Answer the questions below regarding the electric field along a line which is drawn through the middle of the two glass rods (labeled Bisector in the diagram).

(Figure 1)

Homework Equations


*See attached file for relevant equations*

The Attempt at a Solution



Length = 0.113 m
λ = 9.20×10^−8 C/m
Eo = 8.85*10^-12
r1 = 0.037m
r2 = 0.01m

Using the attached equation... I got -1.21*10^5 N/C ... the magnitude of the field is 1.21*10^5 N/C

I know this is wrong but I am confused as to why?
 

Attachments

  • 222-5-1_Glass_Rods.png
    222-5-1_Glass_Rods.png
    1.6 KB · Views: 410
  • Capture.JPG
    Capture.JPG
    5.2 KB · Views: 384
Physics news on Phys.org
  • #2
Are you allowed to treat the rods as infinitely long?
 
  • #3
TSny said:
Are you allowed to treat the rods as infinitely long?

Honestly, I have no idea. I am confused about how to set this problem up but found this equation in my book.
 
  • #4
TSny said:
Are you allowed to treat the rods as infinitely long?
I would think not though as they gave you the length of the rods ?
 
  • #5
sunnnystrong said:
I would think not though as they gave you the length of the rods ?
I tend to agree with you, that they do not want you to approximate the rods as infinitely long. But the formula for E that you are using is for an infinitely long rod.

Do you have an idea of how to handle the case of a rod of finite length? Are you using calculus in your course?
 

1. What is the definition of electric field magnitude?

The magnitude of the electric field at a point is defined as the strength or intensity of the electric field at that point. It is a measure of the force per unit charge exerted by an electric field on a test charge placed at that point.

2. How is the magnitude of the electric field calculated?

The magnitude of the electric field can be calculated by dividing the force exerted on a test charge by the magnitude of the test charge. This can be represented by the equation E = F/q, where E is the electric field magnitude, F is the force exerted on the test charge, and q is the magnitude of the test charge.

3. What is the unit for electric field magnitude?

The unit for electric field magnitude is Newtons per Coulomb (N/C). This can also be written as Volts per meter (V/m) in terms of electric potential.

4. How does the magnitude of the electric field change with distance from the rod?

The magnitude of the electric field decreases as the distance from the rod increases. This is because the electric field is inversely proportional to the square of the distance from the source, according to Coulomb's law.

5. Can the magnitude of the electric field be negative?

Yes, the magnitude of the electric field can be negative. This would indicate that the electric field is directed in the opposite direction of the positive direction, or that the force on a positive test charge would be in the opposite direction of the electric field. This can occur if there are multiple charged objects present, causing the direction of the electric field to be affected by the combined forces of these objects.

Similar threads

Find the magnitude of the electric field at point P
    • Introductory Physics Homework Help
Replies
5
Views
802
Find the electric field at a point away from two charged rods
    • Introductory Physics Homework Help
Replies
11
Views
2K
Electric field in a rotating rod in a magnetic field
    • Introductory Physics Homework Help
Replies
3
Views
947
Find electric field a distance P from a charged rod
    • Introductory Physics Homework Help
Replies
7
Views
1K
Find the direction and magnitude of an electric field
    • Introductory Physics Homework Help
Replies
7
Views
2K
What is the magnitude and direction of the electric field
    • Introductory Physics Homework Help
Replies
23
Views
2K
Electric Field of a cube with a rod
    • Introductory Physics Homework Help
Replies
5
Views
3K
(Help) Surface charge density (σ) for particle to hit plate...
    • Introductory Physics Homework Help
Replies
4
Views
238
Electric field at a point (point charge and semi-circle rod)
    • Introductory Physics Homework Help
Replies
3
Views
5K
Electric field of bent non conducting rod
    • Introductory Physics Homework Help
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top