What is the Maximum Ratio of m1 to m2 to Keep m1 Stationary in a Pulley System?

[Karol]

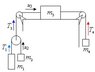
Homework Statement

[/B]
m₁ must stay in place. express m₄ with the rest.
What must be the maximum ratio $\frac{m_1}{m_2}$ in order m₁ will stay in place.

Homework Equations

Mass-acceleration: F=ma

The Attempt at a Solution

2 cases, in the first $m_1<m_2$, which is drawn above:
$$T_1=m_1g,~~m_2g-T_1=m_2a_2~~\rightarrow~~a_2=\left( \frac{m_2-m_1}{m_2} \right)g$$
$$\frac{1}{2}a_2=a_3,~~2T_1=T_3,~~T_3-T_4=m_3a_3~~\rightarrow~~T_4=2T_1-\frac{1}{2}m_3a_3$$
$$T_4-m_4g=m_4a_3~~\rightarrow~~m_4=\frac{T_4}{a_3+g}=\frac{4m_1m_2-(m_2-m_1)m_3}{3m_2-m_1}$$
Since here $m_1<m_2$ the denominator of m₄ is positive, so the nominator must be positive too:
$$4m_1m_2>(m_2-m_1)m_3,~~\frac{m_1}{m_2}\triangleq k~~\rightarrow~~k>\frac{m_3}{4m_2+m_3}$$
In the second scenario $m_1>m_2$:

$$T_1-m_2g=m_2a_2~~\rightarrow~~a_2=\left( \frac{m_1-m_2}{m_2} \right)g$$
$$T_4-T_3=m_3a_3~~\rightarrow~~T_4=2T_1+\frac{1}{2}m_3a_3$$
$$m_4g-T_4=m_4a_3~~\rightarrow~~m_4=\frac{T_4}{g-a_3}=\frac{4m_1m_2+(m_1-m_2)m_3}{3m_2-m_1}$$
Since here $m_1<m_2$ the nominator is positive so the also must be the denominator, thus:
$$m_2-m_1~~\rightarrow~~\frac{m_1}{m_2}<3$$
Which doesn't make sense since the ratio doesn't include m₃ or m₄ at least, as in the previous case.

 

[haruspex]

$-\frac 12m_3a_3$

Where did that 1/2 come from?

Edit: I guess that was just a transcription error. Later lines look ok.

In case 1 you found a lower bound for m₁/m₂. I see no contradiction. You were only asked for an upper bound.

 

[Karol]

$$\left\{\begin{array}{l} T_3-T_4=m_3a_3 \\ 2T_1=T_3 \\ \frac{1}{2}a_2=a_3 \end{array}\right.~~\rightarrow~~T_4=2T_1-\frac{1}{2}m_3a_2$$

In case 1 you found a lower bound for m1/m2. I see no contradiction. You were only asked for an upper bound.

But why doesn't $\frac{m_1}{m_2}<3$ include at least one of the rest? doesn't the second scenario depend on them also?

 

[haruspex]

$$\left\{\begin{array}{l} T_3-T_4=m_3a_3 \\ 2T_1=T_3 \\ \frac{1}{2}a_2=a_3 \end{array}\right.~~\rightarrow~~T_4=2T_1-\frac{1}{2}m_3a_2$$

But why doesn't $\frac{m_1}{m_2}<3$ include at least one of the rest? doesn't the second scenario depend on them also?

It depends how you read the question.
If you read it as finding the max ratio such that a set of masses exists satisfying the condition then you get (anything up to but not including) 3.
If you read it as the max ratio given the masses m₂, m₃, m₄ then you get that it is less than (3m₄+m₃)/(4m₂+m₃+m₄).

 

[Karol]

If you read it as the max ratio given the masses m2, m3, m4 then you get that it is less than (3m4+m3)/(4m2+m3+m4).

$$m_4=\frac{4m_1m_2-(m_2-m_1)m_3}{3m_2-m_1}~~\rightarrow~~4m_1m_2+m_1m_3+m_1m_4=m_2m_3+3m_2m_4$$
$$\frac{4m_1m_2+m_1m_3+m_1m_4}{m_2}=\frac{m_2m_3+3m_2m_4}{m_2}=4m_2\frac{m_1}{m_2}+m_3\frac{m_1}{m_2}+m_4\frac{m_1}{m_2}=m_3+3m_4$$
$$(4m_2+m_3+m_4)\frac{m_1}{m_2}=m_3+3m_4~~\rightarrow~~\frac{m_1}{m_2}=\frac{m_3+3m_4}{4m_2+m_3+m_4}$$
Why, specifically, $\frac{m_1}{m_2}<...$ and not $\frac{m_1}{m_2}>...$?
I didn't see that both scenarios yield the same equation $m_4=\frac{4m_1m_2-(m_2-m_1)m_3}{3m_2-m_1}$. but from this equation i can deduce other things.
First scenario:
$$m_1<m_2~~\rightarrow~~3m_2-m_1>0~~\rightarrow~~4m_1m_2-(m_2-m_1)m_3>0~~\rightarrow~~\frac{m_1}{m_2}>\frac{m_3}{m_3+4m_2}$$
Second scenario:
$$m_1>m_2~~\rightarrow~~or\left\{\begin{array}{l} 3m_2-m_1>0~~\rightarrow~~4m_1m_2-(m_2-m_1)m_3>0~~\rm{exists~for~all~m_i} \\ 3m_2-m_1<0~~\rightarrow~~4m_1m_2-(m_2-m_1)m_3<0~~\rm{cannot~be} \end{array}\right.$$
Does all this derivation apply to your:

If you read it as finding the max ratio such that a set of masses exists satisfying the condition then you get (anything up to but not including) 3.

And also, if i just want that to happen, i have to: $3m_2-m_1\neq 0$

 

[haruspex]

Why, specifically, $\frac{m_1}{m_2}<$...?

Because there is a numerical upper bound (3) but no numerical lower bound greater than zero. If you make m₃ and m₄ arbitrarily small compared to m₂ you can make m₁/m₂ arbitrarily close to 0.

Does all this derivation apply to your:

Yes, we are saying the same there.

 

[Karol]

Because there is a numerical upper bound (3) but no numerical lower bound greater than zero. If you make m3 and m4 arbitrarily small compared to m2 you can make m1/m2 arbitrarily close to 0.

Why upper limit? in the scenario where $m_1>m_2$ i can make m₃ and m₄ big and they will pull up the pulley

 

[haruspex]

Why upper limit? in the scenario where $m_1>m_2$ i can make m₃ and m₄ big and they will pull up the pulley

The ratio m₁/m₂ can never exceed 3. Look at how the expression on the right varies as you change m₂, m₃ and m₄. To maximise it you need a large m₄ compared to m₂ and m₃. As m₄ tends to infinity, what does the expression tend to?

 

[Karol]

As m4 tends to infinity, what does the expression tend to?

$$\frac{m_1}{m_2}=\frac{3\infty}{\infty}=3$$
But now i don't understand what i have done in:
$$m_1<m_2~~\rightarrow~~3m_2-m_1>0~~\rightarrow~~4m_1m_2-(m_2-m_1)m_3>0~~\rightarrow~~\frac{m_1}{m_2}>\frac{m_3}{m_3+4m_2}$$
$$for:~m_3\rightarrow 0~~\Rightarrow~~\frac{m_1}{m_2}\rightarrow 0$$
If m₃ is small, and $m_1<m_2$, m₄ must be small but it doesn't appear.

 

[haruspex]

If m3 is small, and m1<m2, m4 ... doesn't appear.

As you wrote in post #5, the full equation is the same in both cases. In your analysis of m1<m2, you used that to get rid of m4 before letting m3 tend to zero. It only looks different because your analysis followed a different sequence.

 

[Karol]

I thank you very much Haruspex