What is the Net Charge on a Suspended Plastic Ball in an Electric Field?

[cy19861126]

Homework Statement

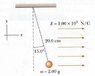
A small 2.00-g plastic ball is suspended by a 20.0-cm-long string in a uniform electric field, as shown in the below diagram. If the ball is in equilibrium when the string makes a 15.0 degree angle with the vertical as indicated, what is the net charge on the ball? If you can't see the diagram below, please go to http://students.washington.edu/cy1126/15.38.jpg

Homework Equations

F = Eq
F = mg

The Attempt at a Solution

I drew the free body diagram and identified three forces, weight, tension and electric force. Direction of the weight points down, electric force to the right and tension to the northwest. Since the electric force is parallel to the x-axis, we would not need to worry about the y direction. So my equation came out to be:
Fx = 1.00^3N/C*q - (0.002kg)(9.8N/kg)(sin 15)
0 = 1.00^3N/C*q - 6.70^-5N
q = 6.7*10^-8C

Okay, the number looks okay, but I feel like it's wrong. This is supposed to be a difficult problem, as marked in the book, but I solved it in one step. Moreover, I did not use the 20cm from the problem. Can anyone take a look at my calculation and see what I did wrong?

 

[hage567]

You need to consider forces in the y direction, so you can find the tension in the string. You did not take that into consideration in your solution.

 

[cy19861126]

You need to consider forces in the y direction, so you can find the tension in the string. You did not take that into consideration in your solution.

I put the tension in the x direction into the equation already. I do not think there is a need to worry about the y direction because the electric field is on the parallel direction and so net charge on the ball only exists on the x direction

 

[hage567]

If you have your coordinate system defined as in the picture, the tension acts at an angle to that system. Therefore, the tension must be resolved into its components in the x and y direction. The electric field may only be in x direction, but the tension in the string is not only all in the x direction as well. Only a certain amount of it will be, and to find that amount, you must consider the forces in the y direction.

Fx = 1.00^3N/C*q - (0.002kg)(9.8N/kg)(sin 15)

This term is not quite right. This is not the tension. Since gravity acts straight down (-ve y direction), there is no component of gravity in your x-direction.
To find the tension, you must sum the forces in the y direction as well. You will then have two equations with two unknowns.

 

[cy19861126]

If you have your coordinate system defined as in the picture, the tension acts at an angle to that system. Therefore, the tension must be resolved into its components in the x and y direction. The electric field may only be in x direction, but the tension in the string is not only all in the x direction as well. Only a certain amount of it will be, and to find that amount, you must consider the forces in the y direction.

Fx = 1.00^3N/C*q - (0.002kg)(9.8N/kg)(sin 15)

This term is not quite right. This is not the tension. Since gravity acts straight down (-ve y direction), there is no component of gravity in your x-direction.
To find the tension, you must sum the forces in the y direction as well. You will then have two equations with two unknowns.

Gocha, but I still did not use the 20cm part from the question. I did the way you suggested:

For the x direction:
1*10^3N/C*q - T*sin 15 = 0

For the y direction:
Tcos15 - 0.002kg*9.8N/kg = 0

Solution: T = 0.0203N
q = 5.18*10^-6C

I still have doubt about my answer. The problem looks more sense now, thanks to hage567, but I am still worried about the 20cm part. I never get to use that number in this problem

 

[hage567]

"but I am still worried about the 20cm part. I never get to use that number in this problem"

Yeah, me either. I'm pretty sure it isn't necessary.

 

[imranq]

I believe since

\displaystyle {PE} (electric) = -qEd

and

\displaystyle {PE} (gravitational) = mgh

thus find the gravitational potential energy by finding the displacement in the y direction (use .2*cosine 15)

then find what E*d is by the displacement in the x-direction (use .2*sine 15).

then by simple algebra calculate 'q'. I believe the 20 cm is necessary

 

[hage567]

I believe since

\displaystyle {PE} (electric) = -qEd

and

\displaystyle {PE} (gravitational) = mgh

thus find the gravitational potential energy by finding the displacement in the y direction (use .2*cosine 15)

then find what E*d is by the displacement in the x-direction (use .2*sine 15).

then by simple algebra calculate 'q'. I believe the 20 cm is necessary

I don't think this is correct. How does this take into account the tension in the string? The tension is part of what is keeping it in equilibrium.

 

[cy19861126]

I believe since

\displaystyle {PE} (electric) = -qEd

and

\displaystyle {PE} (gravitational) = mgh

thus find the gravitational potential energy by finding the displacement in the y direction (use .2*cosine 15)

then find what E*d is by the displacement in the x-direction (use .2*sine 15).

then by simple algebra calculate 'q'. I believe the 20 cm is necessary

Sorry, but I don't think this is right. In this chapter, we have not yet gone over electrical potential energy.

 

[Leperkhan]

I know I am digging up old bones, but I know lots of people who look up old answers in these forums looking for soom guidance, so I'm going to go through this problem.

m=.002 kg
Pheta=15 degrees
F=Eq
F=mg
E=1000 N/C
g=9.8 m/s^2
q=?

Sum of the Forces in the x-direction= Eq-Tsin(Pheta)=0

Sum of the Forces in the y-direction= Tcos(Pheta)-mg=0

T=(mg)/(cos(Pheta)

So sum of the forces in the x-direction=Eq-mgTan(Pheta)=0

q=(mgTan(Pheta)/E)

q=((.002)(9.81)Tan(15 degrees))/1000= 5.26X10^-6

I actually wanted to help in figuring this one out, but I think this old post gave me enough to go on. If anyone thinks what I did is wrong, please say so. Also, I agree the length of the rope is not important.

 

[ShadowGMR420]

I know I am digging up old bones, but I know lots of people who look up old answers in these forums looking for soom guidance, so I'm going to go through this problem.

m=.002 kg
Pheta=15 degrees
F=Eq
F=mg
E=1000 N/C
g=9.8 m/s^2
q=?

Sum of the Forces in the x-direction= Eq-Tsin(Pheta)=0

Sum of the Forces in the y-direction= Tcos(Pheta)-mg=0

T=(mg)/(cos(Pheta)

So sum of the forces in the x-direction=Eq-mgTan(Pheta)=0

q=(mgTan(Pheta)/E)

q=((.002)(9.81)Tan(15 degrees))/1000= 5.26X10^-6

I actually wanted to help in figuring this one out, but I think this old post gave me enough to go on. If anyone thinks what I did is wrong, please say so. Also, I agree the length of the rope is not important.

Thank you so much! You have no idea how much this helped me. I've been stuck on a problem similar to this one for a while.

 

[Leperkhan]

Yeah, no problem... we're in this together. I get inspired with a good answer every once in a while, so I just like giving back. It's funny, I joined this forum just so I could correct the answer, it was bothering me.