musicfairy
- 101
- 0
In the figure below, the charge on a neutral isolated conductor is separated by a nearby positively charged rod. What is the net flux through each of the five Gaussian surfaces shown in cross section? Assume that the charges enclosed by S1, S2, and S3 are equal in magnitude.
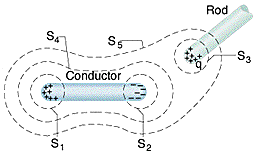
Surface 1:
Surface 2:
Surface 3:
Surface 4:
Surface 5:
I don't know what to do, so I'll need someone(s) to guide me through the process.
I'm guessing I'll have to use the equations
Φ= q/ε0
I really don't know this stuff well, so I can't show much work as of now. That's why I'm trying to find someone who's willing to explain to me a step at a time.
First of all how do I know what sign it is? If it's negative does it mean the sign of q/ε0 is negative? Like S2 would be −q/ε0?
And for S4 would Φ = 0 because it contains S1 and S2 and they have opposite charges?
Surface 1:
Surface 2:
Surface 3:
Surface 4:
Surface 5:
I don't know what to do, so I'll need someone(s) to guide me through the process.
I'm guessing I'll have to use the equations
Φ= q/ε0
I really don't know this stuff well, so I can't show much work as of now. That's why I'm trying to find someone who's willing to explain to me a step at a time.
First of all how do I know what sign it is? If it's negative does it mean the sign of q/ε0 is negative? Like S2 would be −q/ε0?
And for S4 would Φ = 0 because it contains S1 and S2 and they have opposite charges?