What is the point in having a voltage follower?

[theBEAST]

Solving for the voltage gain of an inverting op amp

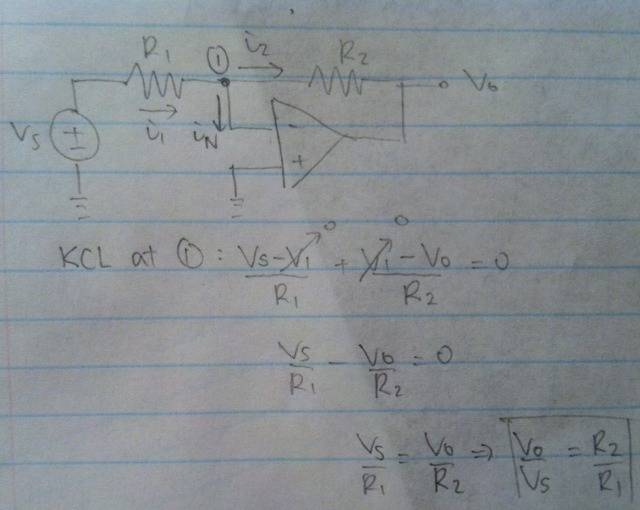
Homework Statement

Find the gain for an inverting op amp.

3. The Attempt at a Solution
I tried to solve for the gain but I ended up getting a positive gain. I think I made a mistake with the current directions but I always thought that when doing nodal analysis, it doesn't matter what direction your current arrows are? Since the math should always work out? I am not too sure... What am I doing wrong?

 

[lewando]

It does matter what direction your current arrows are. KCL states the currents going into a node are zero. You show one current going into the node and the other going out from the node. Change the direction of the second one and you will have your inverter.

 

[theBEAST]

It does matter what direction your current arrows are. KCL states the currents going into a node are zero. You show one current going into the node and the other going out from the node. Change the direction of the second one and you will have your inverter.

Thanks! Also what happens if I were to flip the op amp. In other words switch the terminals so that the - terminal is connected directly to the ground?

 

[lewando]

You will be using the op amp in a way that does not use negative feedback then. The output will "rail" towards the positive supply voltage.

 

[theBEAST]

You will be using the op amp in a way that does not use negative feedback then. The output will "rail" towards the positive supply voltage.

When you say rail, you mean that the output would be the same as the supply voltage right? As in it saturates? But I don't understand how this works, wouldn't the derivation be the same as what I did above with the voltage at node 1 to be 0V?

 

[lewando]

When you say rail, you mean that the output would be the same as the supply voltage right? As in it saturates?

For an ideal op amp analysis, the output would be at the positive supply voltage. For real op amps, the output would not exactly get there but could get close if you were to use a "rail to rail" type op amp.

But I don't understand how this works, wouldn't the derivation be the same as what I did above with the voltage at node 1 to be 0V?

You asked what if you flipped the op amp (reverse the +/- terminals: - is at ground, + is at node 1). In this configuration, you are using positive feedback. Recall the open loop op amp gain equation:

v_out = Gain_{open_loop}*(v₊ - v_-).

If v₊ - v_- becomes slightly positive, the output will become much more positive, contributing additionally to the voltage at v₊, making the output become even more positive, and so on until the rail is reached.