What is the point of convergence for a recursive sequence in a plane?

[toothpaste666]

Homework Statement

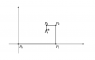
Let $\{P_i\}_{i=0}^\infty$ be a sequence of points on a plane. Suppose $P_i$s are placed as on the picture below, so that $|P_0 P_1|=2, |P_1 P_2|=1, |P_2 P_3|=.5, |P_3P_4|=.25$, ... Find the coordinate of the point $P = \lim_{i→\infty} P_i$

Homework Equations

The Attempt at a Solution

here are the points $P_0: (0,0) P_1: (2,0) P_2: (2, 1) P_3: (1.5, 1) P_4: (1.5, .75) P_5: (1.625, .75)$

lets examine the x values first:
2, 1.5, 1.625

this is a sequence defined recursively by:

$a_1 = 2$

$a_{n+1} = 2 - \frac{a_n}{4}$

$L = \lim_{a_n\rightarrow\infty} a_n = \lim_{a_n\rightarrow\infty} a_{n+1} <br /> = \lim_{an\rightarrow\infty} 2-\frac{a_n}{4}$

which means that

$L = 2-\frac{L}{4}$

$4L = 8 - L$

$5L = 8$

$L = \frac{8}{5}$

$L = 1.6$

so 1.6 would be the x coordinate of the point.

I then would follow a similar process to find the y coordinate, but before I do that I just want to make sure what I have so far is correct.

 

[toothpaste666]

also forgive me for not proving the sequence is bounded and decreasing (I left it out to save time and narrow the focus) but i have done so by mathematical induction

 

[dirk_mec1]

Yes it is correct but also prove it is bounded and decreasing.

 

[toothpaste666]

Ok so it turns out one of my induction proofs was wrong. I can prove it is bounded but this sequence is not strictly increasing or decreasing. it hops back and forth between increasing and decreasing but it IS approaching a certain point. Is there any way to prove that it has a limit?

 

[toothpaste666]

the proof that it is bounded:

$1 ≤ a_n ≤ 2$

$\frac{1}{4} ≤ \frac{a_n}{4} ≤ \frac{2}{4}$

$-\frac{1}{4} ≥ -\frac{a_n}{4} ≥ -\frac{2}{4}$

$2-\frac{1}{4} ≥ 2-\frac{a_n}{4} ≥ 2-\frac{2}{4}$

$1.75 ≥ a_{n+1} ≥ 1.5$

$1 ≤ 1.5 ≤ a_{n+1} ≤ 1.75 ≤ 2$

$1 ≤ a_{n+1} ≤ 2$