What is the relationship between weight and length in a cord and pulley problem?

[cwill53]

Homework Statement

The cord CAEBD passes over pulleys A and B of negligibly small diameter. Two weights of p lbs each are attached to the ends C and D of the cord, and a weight of P lbs to the point E of the same cord. The points A and B are at the same level and the span AB is $l$. Determine the distance $x$ between the level AB and the point E if the system is in equilibrium, neglecting friction and the weight of the cord.

Answer:
$$x=\frac{Pl}{2\sqrt{4p^2-P^2}}$$

Relevant Equations

$$\sum \vec{F}=m\vec{a}$$

I've deduced that the weight of each weight p is half that of the weight P, and likewise P= 2p.
Here's the diagram for the problem:

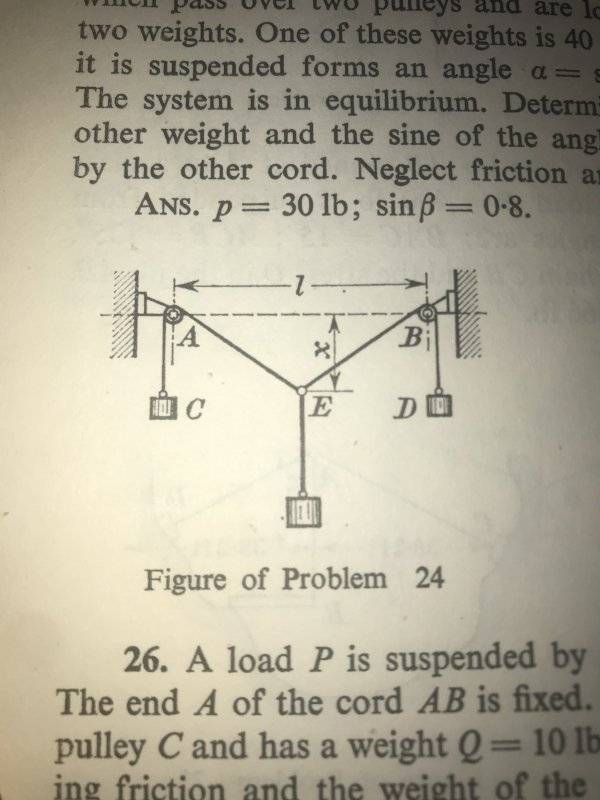
As you can see, the length x is equal to the height of the triangle AEB.
I know that if a triangle has equal sides of length $a$ and a base of length $b$, the height h can be simplified to:
$$h=\frac{1}{2}\sqrt{4a^2-b^2}$$

I just don't see how to find the sides $a$, which are AE and EB in this example, in terms of the weights, and the proportionality/relationship between the weights and these lengths.

 

[haruspex]

I've deduced that the weight of each weight p is half that of the weight P

A remarkable achievement.
Did you notice that according to the book answer that makes x infinite?

 

[cwill53]

A remarkable achievement.
Did you notice that according to the book answer that makes x infinite?

No. If that’s the case I don’t know how to solve the problem.
When I try to solve these problems I try not to keep the answer in mind.

 

[haruspex]

No. If that’s the case I don’t know how to solve the problem.
When I try to solve these problems I try not to keep the answer in mind.

Ok, but it means your deduction was wrong, and you have not explained how you deduced it.
The usual way to solve an equilibrium problem is to write equations expressing the balance of forces. Create variables for the tensions and write those equations.

 

[cwill53]

Ok, but it means your deduction was wrong, and you have not explained how you deduced it.
The usual way to solve an equilibrium problem is to write equations expressing the balance of forces. Create variables for the tensions and write those equations.

What I got was that the x-components cancel and you have for the y direction:

p lbs + p lbs = P lbs

I also see that the sides AE and EB are equal to $\frac{\sqrt{4x^2-l^2}}{2}$.

Does 2p = -P?

 

[haruspex]

the x-components cancel

Yes.

for the y direction: p lbs + p lbs = P lbs

I already indicated that is wrong, and you are still not providing any basis for that claim.
What are the tensions in the cords? What is the vertical balance equation at the point where they meet?

 

[cwill53]

Yes.

I already indicated that is wrong, and you are still not providing any basis for that claim.
What are the tensions in the cords? What is the vertical balance equation at the point where they meet?

The basis was the y equation I gave in the last comment. I don’t see what other forces are involved besides P and the two loads of p.
Wouldn’t the tension in the cords each be (P/2)-p?

 

[haruspex]

The basis was the y equation I gave in the last comment.

Your starting equations must be based on physical laws. Your equation in post #5 appears out of nowhere.

Wouldn’t the tension in the cords each be (P/2)-p?

No.
Try to answer these questions in sequence:

1. What is the tension in the vertical section of cord above the left hand weight?
2. What is the tension in the angled section of cord from the left hand pulley to the knot where the cords meet?
3. What is the tension in the vertical section of cord above the central weight?
4. What forces act at the knot?
5. What are the vertical components of those forces?
6. What equation represents the vertical balance of forces at the knot?

 

[cwill53]

Your starting equations must be based on physical laws. Your equation in post #5 appears out of nowhere.

No.
Try to answer these questions in sequence:

1. What is the tension in the vertical section of cord above the left hand weight?
2. What is the tension in the angled section of cord from the left hand pulley to the knot where the cords meet?
3. What is the tension in the vertical section of cord above the central weight?
4. What forces act at the knot?
5. What are the vertical components of those forces?
6. What equation represents the vertical balance of forces at the knot?

I got $T_{AC}=p$

How do you find number 2? I don't quite understand how the forces of p and the centerweight are interacting.

 

[wrobel]

the shortest way is to find critical points of the potential energy I guess

 

[cwill53]

the shortest way is to find critical points of the potential energy I guess

I'm not sure how to solve the problem as there are no angles for me to find the components of the tensions in BE and AE with.

 

[haruspex]

I'm not sure how to solve the problem as there are no angles for me to find the components of the tensions in BE and AE with.

You don't need the angles as such, just their sines and cosines. You have those in the form of x and L.

 

[Lnewqban]

No. If that’s the case I don’t know how to solve the problem.
When I try to solve these problems I try not to keep the answer in mind.

Perhaps this could help you:
https://www.engineeringtoolbox.com/wire-rope-slings-d_1613.html

The angle respect to a vertical line (direction of the gravity force) formed by the sections AE and BE of the rope makes the magnitude of the tension of each be greater than half the weight of the central mass P.

The smaller height x becomes respect to distance l, the bigger those tensions become, up to the theoretical value of infinite if x could become zero.

Rather than having those pulleys and equal masses p keeping the system in equilibrium (the big mass P stays suspended in midair), imagine you and a friend would be pulling from ropes AE and BE each.

You would soon note that the higher you try to keep mass P, the harder each of you would need to pull the rope.
You would never be able to keep sections AE and BE on a horizontal line, certain triangle ABE would naturally form, no matter how hard you both pull.

You could also feel that allowing the mass P to descend would reduce the individual pulling effort, which only then would tend to be half the weight of mass P.
Therefore, for keeping a triangle ABE of proportions similar to the one shown in the schematic, each mass p must weight much more than half the weight of mass P.

 

[cwill53]

You don't need the angles as such, just their sines and cosines. You have those in the form of x and L.

Is p the vertical component of force of the in each of the two sections of the rope AE and BE?

If it is that means that P would be equal to $2psin\alpha$, where $\alpha$ is the angle between AE and CE, equal to the angle between BE and DE.

 

[haruspex]

Is p the vertical component of force of the in each of the two sections of the rope AE and BE?

No.
You got the tension in AC correctly as being p. How should that relate to the tension in AE? Think about the pulley at A. If the two tensions are not equal, what will happen?

 

[cwill53]

No.
You got the tension in AC correctly as being p. How should that relate to the tension in AE? Think about the pulley at A. If the two tensions are not equal, what will happen?

If the two tensions weren't equal, there would be a net force and therefore acceleration in the system.
P would still be equal to $2psin\alpha$, $\alpha$ being the angle between the AE and CE which is equal to the angle between BE and DE, right?

 

[cwill53]

I finally figured it out, I'll post this for anyone stuck on a similar problem.

$$y:T_{AC}=T_{BD}=T_{AE}=T_{BE}=p$$
$$-P+2psin\alpha \Rightarrow P=2psin\alpha $$
$$psin\alpha \propto x; pcos\alpha \propto \frac{l}{2}$$
$$P=2p(\frac{x}{\sqrt{x^{2}+\frac{l^{2}}{4}}})$$
$$\frac{P\sqrt{x^{2}+\frac{l^{2}}{4}}}{2p}=x\Rightarrow P^{2}(x^2+\frac{l^2}{4})=4p^2x^2$$

$$\frac{x^2}{x^2+\frac{l^2}{4}}=\frac{P^2}{4p^2}\rightarrow x^2=\frac{P^2x^2+\frac{P^2l^2}{4}}{4p^2}\Rightarrow x^2(4p^2-P^2)=\frac{P^2l^2}{4}$$

$$x^2=\frac{P^2l^2}{4(4p^2-P^2)}\Leftrightarrow x=\frac{Pl}{2\sqrt{4p^2-P^2}}$$