What is the second term of the total kinetic energy in a rigid pendulum system?

[fib1123]

Homework Statement

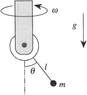
The bearing of a rigid pendulum of mass is forced to rotate uniformly
with angular velocity (see Figure P. 1.32). The angle between the rotation
axis and the pendulum is called θ.Neglect the inertia of the bearing and of
the rod connecting it to the mass. Neglect friction. Include the effects of
the uniform force of gravity.

Homework Equations

What represents the second term of the total kinetic energy of the system?

The Attempt at a Solution

I used the lagrangian mechanics to solve the problem.

 

[haruspex]

What represents the second term of the total kinetic energy of the system?

At any instant, we can resolve the motion of the bob into two orthogonal motions, both perpendicular to the pendulum rod: a horizontal velocity normal to the vertical axis and a velocity in the vertical plane through the rod. These correspond to the two KE terms.