Juntao
- 45
- 0
I've added a picture as an attachment.
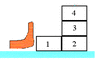
Four blocks of mass m = 10 kg are arranged as shown in the picture, on top of a frictionless table. A hand touching block 1 applies a force of F1h = 90 N to the right. The coefficient of friction between the blocks is sufficient to keep the blocks from moving with respect to each other.
What is the total force exerted on block 3 by block 2 ?
---------------------------------------------------------
Ok. This is what my force diagram for object 3 looks like.
Imagine a box. There is an arrow pointing from the top of the box upwards. This is the normal force put on block 3 by block 2.
I have a normal force pointing down put on block 3 by block 4. There is also a W (weight of block 4) pointing down also.
To the right, I have a friction force put on block 3 by block 2, and to the left, I have another friction force put on block 3 by block 4.
Also, I did a force diagram with block 4. A normal pointing up from block 3, a friction force to the right from block 3, and a W pointing down.
Through some analysis, I know that the normal force on block 3 by block 2 is equal to twice the normal force put on block 3 by block 4.
Likewise, the friction force put on block 3 by block 2 is equal to twice the friction force put on block 3 by block 4.
It's twice the normal and friction because block 4 has to put force through two blocks to get to block 2 (hope that makes sense).
And I know that w=m*g=(10kg)(9.8m/s/s)=98 N.
---------------------------------------------
Now I'm pretty much stuck. I know that I could combine block 3 and block 4 so it is one big block 3, but after that, I don't know how to calculate the net force onto block 2. I'm still trying to get the hang of forces.
Four blocks of mass m = 10 kg are arranged as shown in the picture, on top of a frictionless table. A hand touching block 1 applies a force of F1h = 90 N to the right. The coefficient of friction between the blocks is sufficient to keep the blocks from moving with respect to each other.
What is the total force exerted on block 3 by block 2 ?
---------------------------------------------------------
Ok. This is what my force diagram for object 3 looks like.
Imagine a box. There is an arrow pointing from the top of the box upwards. This is the normal force put on block 3 by block 2.
I have a normal force pointing down put on block 3 by block 4. There is also a W (weight of block 4) pointing down also.
To the right, I have a friction force put on block 3 by block 2, and to the left, I have another friction force put on block 3 by block 4.
Also, I did a force diagram with block 4. A normal pointing up from block 3, a friction force to the right from block 3, and a W pointing down.
Through some analysis, I know that the normal force on block 3 by block 2 is equal to twice the normal force put on block 3 by block 4.
Likewise, the friction force put on block 3 by block 2 is equal to twice the friction force put on block 3 by block 4.
It's twice the normal and friction because block 4 has to put force through two blocks to get to block 2 (hope that makes sense).
And I know that w=m*g=(10kg)(9.8m/s/s)=98 N.
---------------------------------------------
Now I'm pretty much stuck. I know that I could combine block 3 and block 4 so it is one big block 3, but after that, I don't know how to calculate the net force onto block 2. I'm still trying to get the hang of forces.