pitaaa
- 20
- 0
Homework Statement
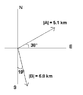
Determine the vector that must be added to the sum of A + B in the given attachment to give a resultant displacement of (a) O and (b) 4.0 km [W]. In case anyone can't view the attachment, |A| is 5.1 km in length, 38 degrees N of E, and |B| is 6.8 km in length, 19 degrees E of S, both attached tail-to-tail.
Homework Equations
∆d = d1 + d2 + ...
c^2 = a^2 + b^2 -2abcosC
The Attempt at a Solution
So, in order to get a displacement of zero, your resultant has to be at the initial point, so I simply drew a vector from the end of |A| to the end of |B| and obtained the answer 7.0 km, which is the answer in the book. Where I'm a bit lost is where the angle's coming from? The answer in the book is 28 degrees N of W - I don't know where I'm supposed to indicate this angle from. I'm also a lost on part (b), where the resultant is 4.0 km [W]... I don't even know where to begin on that one. I've drawn my diagram - the 4.0 km is branching from the end of |B| in the direction of West, and I know the vector I'm looking for is from the end of |A| to the end of the 4.0 km one, I just don't know how to go about calculating it, other than drawing a scale diagram.
Any insight is sincerely appreciated !