Adesh
- 735
- 191
- Homework Statement
- Find the acceleration of block A and block B.
- Relevant Equations
- $F=ma$.
Find the acceleration of block A and B, given that the mass of pulleys and strings are negligible.
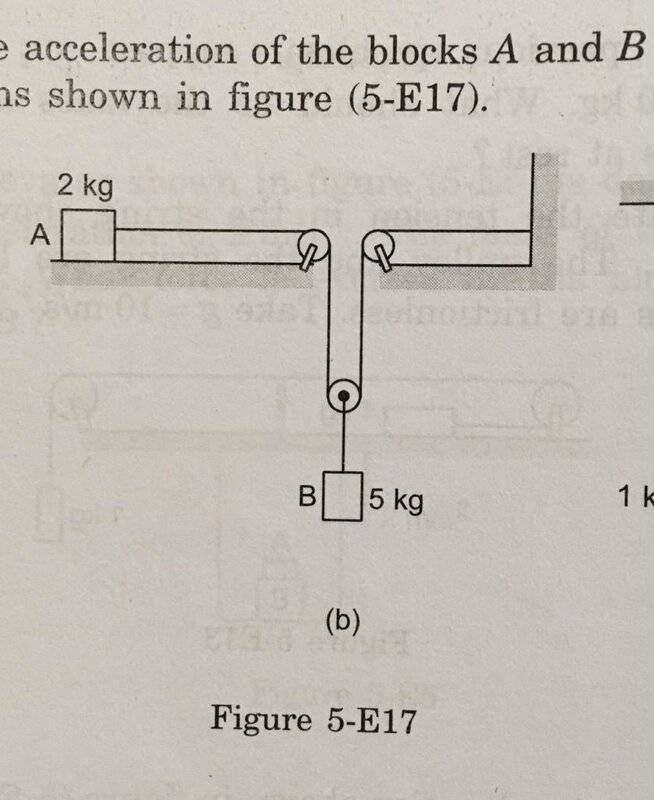 . I could see that the block B has gravity acting on it, therefore the gravitational force on the block ##B## is ##F_B = 5 g## and hence the acceleration is ##g##. From the pulley to which block B is connected there goes two strings, therefore tension on each string will be half of ##F_B##, therefore the force on the block ##A## is ##F_A = \frac{F_B}{2} = \frac{5g}{2}## and therefore the acceleration of the block ##A## is ##\frac{5g}{4}##. Unfortunately, my answers are wrong, the correct answers are ##\text{acceleration of block A}= \frac{2}{7} g## and ##\text{acceleration of block B}= \frac{g}{7}##.
. I could see that the block B has gravity acting on it, therefore the gravitational force on the block ##B## is ##F_B = 5 g## and hence the acceleration is ##g##. From the pulley to which block B is connected there goes two strings, therefore tension on each string will be half of ##F_B##, therefore the force on the block ##A## is ##F_A = \frac{F_B}{2} = \frac{5g}{2}## and therefore the acceleration of the block ##A## is ##\frac{5g}{4}##. Unfortunately, my answers are wrong, the correct answers are ##\text{acceleration of block A}= \frac{2}{7} g## and ##\text{acceleration of block B}= \frac{g}{7}##.
Can somebody please tell me what's my mistake without just giving out the whole complete solution?
Thank you.
Can somebody please tell me what's my mistake without just giving out the whole complete solution?
Thank you.
