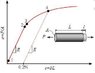
The discussion centers on the interpretation of the broken diagonal line in stress-strain curves for ductile materials, particularly regarding the 0.2% proof stress. This proof stress signifies the stress level at which a material exhibits a permanent set of 0.2% strain after being unloaded. The dashed line represents a new elastic region that parallels the original linear elastic region, indicating that Young's modulus remains consistent despite the material's previous plastic deformation. The choice of 0.2% for proof stress is practical for comparing the elastic and plastic behaviors of different metals. Understanding these concepts clarifies the relationship between stress, strain, and energy in material mechanics.