lillybeans
- 67
- 1
This was on my physics exam today and I couldn't solve it. Switch (two red dots) was originally open, and when it was open, the capacitor is uncharged. Then the switch was closed, and they asked me to find the time constant of the charging process.
I couldn't find the time constant because I couldn't find the Req. I can not reduce this circuit any further into a simple series/parallel resistors configuration. Clearly they are neither in parallel or series with each other. So in this case, how can I calculate the time constant if Req cannot be found (the resistors are neither in parallel or in series)? Do you need differential equations to solve this? Because we haven't learned anything about that in class. (but still teach me please)
P.S. Time constant=RC
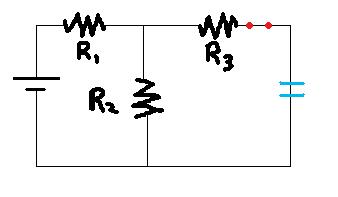
Thanks...
I couldn't find the time constant because I couldn't find the Req. I can not reduce this circuit any further into a simple series/parallel resistors configuration. Clearly they are neither in parallel or series with each other. So in this case, how can I calculate the time constant if Req cannot be found (the resistors are neither in parallel or in series)? Do you need differential equations to solve this? Because we haven't learned anything about that in class. (but still teach me please)
P.S. Time constant=RC
Thanks...
Last edited: