Why Can't I Solve This Static Friction Ladder Problem?

In summary, the problem involves a system of equations involving forces and moments, with the goal of determining the value of μ. The given equations are used to find the value of θ, but there is difficulty in finding the correct value of μ, despite multiple attempts at substitution. Additionally, the angles in the free body diagram may be incorrect and should be corrected to 90-theta.
  • #1
jordan35
4
0

Homework Statement


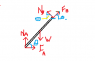
See attachment.


Homework Equations


F = μN

The Attempt at a Solution


I attached the FBD I drew. I then did
ƩFx = FA + FBcosθ - NBsinθ = 0
ƩFy = NA -W + NBcosθ + FBsinθ = 0
ƩMA = 19.5NB - 3.75W = 0
ƩMB = 3.75W - 7.5NA + 18FA = 0
FA = μNA
FB = μNB
θ = arctan(18/7.5) = 67.38°

I know μ is supposed to equal .18, but I can't get it. I've tried substituting different things I don't know how many times now, and I can usually get to an expression of just μ or μ and θ, but I can never get it to equal .18.
 

Attachments

  • Capture.PNG
    Capture.PNG
    10.6 KB · Views: 469
  • Capture2.PNG
    Capture2.PNG
    2.4 KB · Views: 445
Last edited:
Physics news on Phys.org
  • #2
The angles at the wall are wrong on your FBD. They should both be 90-theta.
 

FAQ: Why Can't I Solve This Static Friction Ladder Problem?

1. What is static friction in the context of a ladder problem?

Static friction is a force that keeps an object at rest on a surface, preventing it from moving or sliding. In the case of a ladder problem, static friction refers to the force that keeps the ladder from slipping or falling while in use.

2. How is static friction different from kinetic friction?

Static friction and kinetic friction are two types of friction that act on objects in different ways. Static friction occurs when an object is at rest and prevents it from moving, while kinetic friction occurs when an object is in motion and acts to slow it down.

3. How do you calculate the static friction force in a ladder problem?

The static friction force can be calculated using the formula Fs = μsN, where Fs is the static friction force, μs is the coefficient of static friction, and N is the normal force exerted on the object by the surface.

4. What factors affect the static friction force in a ladder problem?

The static friction force in a ladder problem is affected by the coefficient of static friction, the weight of the ladder and the person on it, and the angle at which the ladder is placed against the surface. The roughness of the surface and the type of material the ladder is made of may also play a role.

5. How can the static friction force be overcome in a ladder problem?

The static friction force can be overcome by increasing the force applied to the ladder, reducing the weight on the ladder, or decreasing the angle at which the ladder is placed against the surface. Alternatively, changing the surface or material of the ladder may also reduce the static friction force.

Similar threads

Inclined Plane Static Friction Coefficient
Replies
11
Views
3K
How can I determine the instant the block overcomes static friction?
2
Replies
61
Views
1K
Why Is My Statics Friction Calculation Incorrect?
Replies
18
Views
3K
Ladder problem (statics) with 2 sources of friction
Replies
2
Views
5K
Find min/max accel. for block to stay on wedge (static fric)
Replies
1
Views
2K
Ladder with 2 forces of friction and a person climbing (statics)
Replies
5
Views
6K
Need help on static friction problem
Replies
2
Views
4K
Dynamics problem involving an inclined plane and Friction
Replies
1
Views
1K
Coefficient of Static Friction = tan (angle of incline)
Replies
4
Views
19K
The greatest angle at which a ladder won't slip
Replies
1
Views
4K

Hot Threads

Recent Insights

Back
Top