Mariah
- 3
- 0
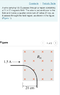
Homework Statement
in the picture.
Homework Equations
F=ILcrossB
Along with the original question, the other picture contains the solution with different numbers. I was just wondering why when finding the force on the wire instead of making dl= R*dtheta and going through the integration and separating the force into to components. Why isn't it possible to simply solve the equation for F=ILBsin90 with L= 2*pi*r/4?