Jae
- 10
- 0
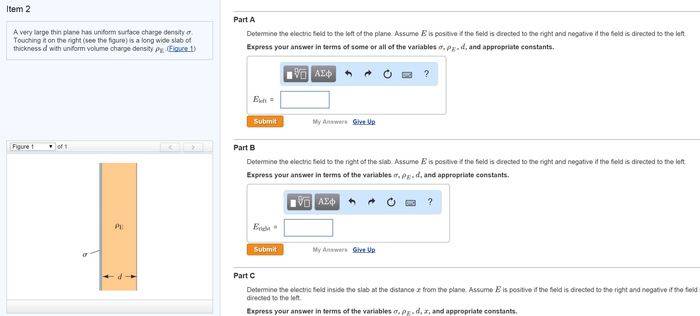
This problem has charge that is not uniform in the inside, but it is still possible to find the electric field as a function of distance outside the slab using Gauss's law. How is this possible if the electric field is not uniform in the slab and plane? Wouldn't the electric field from the middle of the slab to the a x-distance d be different on both sides?
Once I did Gauss's law I got a correct solution of
(sigma + row_E) / 2(epsilon naught)
Thank you for answering this question.
Mentor's Note: Thread moved to Advanced Physics Homework from another forum, hence the lack of a template.
Once I did Gauss's law I got a correct solution of
(sigma + row_E) / 2(epsilon naught)
Thank you for answering this question.
Mentor's Note: Thread moved to Advanced Physics Homework from another forum, hence the lack of a template.
Last edited by a moderator: