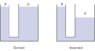B Why is the height of a liquid not affected by the radius of a U-Shaped tube

[AmirWG]

Why the height of liquid is not affected by the radius of U-Shaped tube . ..my textbook says this and it does make sense because if increase the radius of u shaped tube the height of liquid should decrease as the liquids take shape of their container.
Edit : I could not make the title longer...

 

[kuruman]

Please post exactly what the textbook says and preferably show a picture. On the basis of what you say you are right, the larger you make the tube for a fixed amount of liquid, the lower the level of the liquid in the tube. However, there may be more to this so the context of the textbook's statement is important to know.

 

[sophiecentaur]

@AmirWG it is easy to get confused when you try blindly to follow ‘rules’ in Physics. The essence of hydrostatic pressure is the height of fluid involved and not the shape of the container. To get the height, you may need to add or subtract some liquid. There is no confusion if you read what the ‘rule’, ‘law’ or whatever, actually says.

 

[AmirWG]

@kuruman
@sophiecentaur
i am talking about this :

and this ( this is just an example of what i am saying btw)

what does he mean by that ? if we use u shaped tube with two branches with different diameters realistically we should get totally difference results as the branche with smaller diameter will increase the height of the liquid. i just need a clarification of what the textbook is saying
i know my question might look so lame but i am not a physicist.

 

[boneh3ad]

There is no requirement that each side have and equal volume of liquid.

 

[kuruman]

The pressure at a given depth $d$ is the weight of the fluid above that depth divided by the cross-sectional area of the tube, $p=\frac{mg}{A}.$
The mass above that depth is equal to the density of the fluid multiplied by the volume $m=\rho V.$
The volume is the height (same as the depth) of the column times the area, $V=Ad$.
Putting it all together$$p=\frac{mg}{A}=\frac{\rho~ A~ d~g}{A}=\rho~g~d$$Note that the area cancels out therefore the two sides can have different cross-sectional areas yet the pressure will be the same at the same height on each side.

In the figure you posted the pressure is the same at points A and B. The reason the column of fluid is higher above point B is that oil is less dense and therefore the pressure does not vary as rapidly with depth as in water. To get the same pressure as at A you need a higher column of fluid above B.

 

[AmirWG]

The pressure at a given depth $d$ is the weight of the fluid above that depth divided by the cross-sectional area of the tube, $p=\frac{mg}{A}.$
The mass above that depth is equal to the density of the fluid multiplied by the volume $m=\rho V.$
The volume is the height (same as the depth) of the column times the area, $V=Ad$.
Putting it all together$$p=\frac{mg}{A}=\frac{\rho~ A~ d~g}{A}=\rho~g~d$$Note that the area cancels out therefore the two sides can have different cross-sectional areas yet the pressure will be the same at the same height on each side.

In the figure you posted the pressure is the same at points A and B. The reason the column of fluid is higher above point B is that oil is less dense and therefore the pressure does not vary as rapidly with depth as in water. To get the same pressure as at A you need a higher column of fluid above B.

got it , thanks for your time.

 

[sysprog]

In the U-shaped tube, the column of air above the smaller diameter orifice exerts the same pressure as does the column of air as does that above the larger diameter orifice.

Here's another illustration of the same principle in action, from https://www.britannica.com/science/Pascals-principle:

llustration of Pascal's principle at work in a hydraulic press. According to Pascal's principle, the original pressure (P1) exerted on the small piston (A1) will produce an equal pressure (P2) on the large piston (A2). However, because A2 has 10 times the area of A1, it will produce a force (F2) that is 10 times greater than the original force (F1). Through Pascal's principle, a relatively small force exerted on a hydraulic press can be magnified to the point where it will lift a car.
Encyclopædia Britannica, Inc.

 

[kuruman]

I am not sure OP was asking about Pascal's principle. I think OP was asking why the picture on the left is correct and the one on the right is incorrect.

 

[jna]

I think that the OP's intended question has not been answered by any of the above (albeit informative) responses. I think his/her confusion stems from the inaccurate wording in the textbook. The text claims that the height is not affected by the diameter of the tube. Clearly, that is incorrect to say. Given a constant amount of liquid(s), the absolute height (e.g., h_w in his figure) will change if the diameter changes. What will not change is the ratio of the heights in the two branches. So, I have sympathy for the OP and the confusion the ill-worded textbook creates.

 

[kuruman]

I think that the OP's intended question has not been answered by any of the above (albeit informative) responses. I think his/her confusion stems from the inaccurate wording in the textbook. The text claims that the height is not affected by the diameter of the tube. Clearly, that is incorrect to say. Given a constant amount of liquid(s), the absolute height (e.g., h_w in his figure) will change if the diameter changes. What will not change is the ratio of the heights in the two branches. So, I have sympathy for the OP and the confusion the ill-worded textbook creates.

I disagree with your assessment. It seems to me that OP's question has been answered, hence post #7.

got it , thanks for your time.

 

[jna]

I disagree with your assessment. It seems to me that OP's question has been answered, hence post #7.

Maybe, I guess @AmirWG should comment, and I do not mean to diminish your effort answering what you believe was the OP's confusion. All I can say with absolute certainty is that the highlighted wording in the textbook is irritatingly confusing to me.

 

[kuruman]

All I can say with absolute certainty is that the highlighted wording in the textbook is irritatingly confusing to me.

I would agree with that. Note 2 in the book should read "The radius of the tube or the cross sectional area of the two branches doesn't affect the height difference between the levels[/color] of the liquids in the two branches."

 

[jna]

I would agree with that. Note 2 in the book should read "The radius of the tube or the cross sectional area of the two branches doesn't affect the height difference between the levels of the liquids in the two branches."

Not the height *ratio* ?

 

[kuruman]

Not the height *ratio* ?

"Height" is an ambiguous concept here. Height measured from where? I suppose the clear definition of height is "from a horizontal level such that there is liquid on both sides." I was trying to get around the ambiguity of "height" in the picture shown below. When one uses $p=p_0+\rho g h$, $h$ is not a "height" but a depth below a level where the pressure is $p_0$. I have to think about how to rephrase this.

 

[sysprog]

@kuruman, I agree with your earlier point directed at me in this thread that Pascal's principle is not what the OP was asking about -- the U-shaped tube is open, whereas the hydraulic jack is closed.

I also agree that the wording in the text could be confusing, especially the inclarity of the use of the term "height". When there are 2 liquids of different densities at the 2 ends of the tube, with both ends open to the atmosphere, as in the OP's image, you get variance in height of the liquids below the ends of the tube, similarly to, but in this instance more clearly labeled, as in the following image (from an illustration for a fluid statics problem video explanation presented here):



It's a pretty good, reasonably on-topic (I think) video, so I'll leave it linked as a video, but I'll also go ahead and synopsize the diagram:

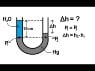
That diagram depicts water, which is of density (as specific gravity) 1, in one end of the tube, and mercury, of density about 13.6, in the other end. With both ends of the tube open to the atmosphere, the water end will be visibly higher above the equal pressure line in the tube, for equal weights of water and mercury above that line, the zero line.

In the diagram, the label says P1 = P2, which makes the line between them horizontal, and makes that line the zero line.

The zero line is set at the lower of the 2 mercury levels, because there's only mercury below that level, therefore only one fluid density, so the heights at that level being the same, the pressures are the same, just as we see equal liquid height in a U-shaped tube when there's only 1 liquid and both ends are open to the atmosphere.

If the water height above P1 is 15 cm, then the mercury height above P2 should be about 1/13.6th of that, or about 1.1 cm (the diagram's not drawn to scale), because mercury is 13.6 times as dense as water. The video explains that calculation in detail. (If instead of using mercury for a barometer you made a water barometer, then instead of atmospheric pressure being about 76.6 cm of Hg, you'd have about 10.4 m. of H2O.) The diagram poses the question what is $\Delta h$ equal to (I'd have called it h1-h2, instead of h2-h1, as on the diagram label); it is the (absolute) difference between the heights above zero of the water and the mercury, meaning 15 cm - 1.1 cm, which is 13.9 cm.

For a single fluid of uniform density, as in the 2 diagrams of pairs of tubes below, you get different heights at the 2 ends of the tube only if there's a difference between the pressures at the 2 ends.

Please note the difference between the use of the term h in the 1st image vs (H) in the second image.

In second of the pair of tubes in that image, P2 > P1, and h refers to how far above the zero line the fluid at the lower-pressure end is.

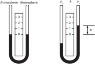
In that image, (H) refers to how far zero is above the lower fluid level, plus how far the higher level is above zero.

One of the (endearing?) bewildering qualities of standard definitions is that there are so many of them to choose from.

 

[sysprog]

Not the height *ratio* ?

The difference in heights is directly proportional to the difference in densities, and densities are ratios (mass per volume).

The height ratio is an equality function of the density ratio, i.e. $\mathtt{h1/h2 = d1/d2}$, and so it does not depend on volume or area; but also, for a given height h1 or h2, the difference between the heights, i.e $\mathtt{|h1-h2|}$, is similarly invariant for any change in area under their heights.

For the 2-liquid problem of the OP, the relative heights of the 2 liquids, and therefore the difference in their heights when one or the other height is given, doesn't change as a function of area; that's a direct function of density. But, as you pointed out in your earlier post, in which you expressed disapprobation of the problem wording in the OP's text, the absolute height of the water column is a function of area as part of volume, which includes both area and height.

Here we're using the term "height" to mean height above the zero line. All of the less-dense liquid is above the zero line. The height of the less-dense liquid, along its density relative to the denser liquid, determines the point of the zero line, and from there the height of the denser liquid.

Given a constant amount of liquid(s), the absolute height (e.g., h_w in his figure) will change if the diameter changes.

If only the denser-liquid end's diameter changes, and that liquid is still of sufficient volume to separate the two ends and to establish cross-sections at the zero line and above, the depth below will not affect, and neither will the diameter across the denser-liquid end affect, the height above the zero line of the less-dense liquid, because all of its height is by definition above the zero point. A broader diameter at the denser liquid end could lower the zero point, but not the height above it of the less-dense liquid.

What will not change is the ratio of the heights in the two branches.

Agree. Given a height, e.g. that of the less-dense liquid, the difference in densities of the 2 liquids is the determinant of the difference in heights between the 2 liquids above the zero point, which point is at the base of the less-dense liquid.