Why Is There a Discrepancy in the Bead and Hoop Velocity Calculations?

[Kelly Lin]

Homework Statement

Homework Equations

The Attempt at a Solution

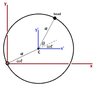
I know we can solve it by letting
<br /> x=acos(\omega t)+acos(\theta+\omega t)\\<br /> y=asin(\omega t)+asin(\theta +\omega t)<br />
and put their derivatives into the Lagrangian.

But, I want to check the other points of view whether it is wrong or something else is missing.
<br /> a\dot{\theta} = v_{\text{bead}}-v_{\text{hoop}}\\<br /> v_{\text{bead}} = a\dot{\theta}+ a\omega<br />
Thus, the Lagrangian will be
<br /> L=\frac{1}{2}m(a\dot{\theta}+ a\omega)^{2}<br />
But, there is a huge difference between two results. Can someone enlighten me? THANKS!

 

[TSny]

a\dot{\theta} = v_{\text{bead}}-v_{\text{hoop}}\\<br /> v_{\text{bead}} = a\dot{\theta}+ a\omega<br />

You can see that something's wrong here by looking at special cases. For example, suppose the bead remains located at the end of the diameter that passes through the origin of the coordinate system. Then $\theta = 0 = \text{constant}$. Your result wold then say that $v_{\text{bead}} = a\omega$. But the speed of the bead in this case would actually be $2a\omega$.

The relative velocity equation can be written as a vector equation: $$\vec v_{\text{bead/XYZ}} = \vec v_{\text{bead/C}} + \vec v_{C/\text{XYZ}}$$ where

$\vec v_{\text{bead/XYZ}}$ = the velocity of the bead relative to the fixed XYZ coordinate system

$\vec v_{\text{bead/C}}$ = the velocity of the bead relative to a non-rotating reference frame moving with the center of the circular hoop

$\vec v_{C/XYZ}$ = the velocity of the center of the hoop with respect to the fixed XYZ coordinate system.

 

[Kelly Lin]

You can see that something's wrong here by looking at special cases. For example, suppose the bead remains located at the end of the diameter that passes through the origin of the coordinate system. Then $\theta = 0 = \text{constant}$. Your result wold then say that $v_{\text{bead}} = a\omega$. But the speed of the bead in this case would actually be $2a\omega$.

The relative velocity equation can be written as a vector equation: $$\vec v_{\text{bead/XYZ}} = \vec v_{\text{bead/C}} + \vec v_{C/\text{XYZ}}$$ where

$\vec v_{\text{bead/XYZ}}$ = the velocity of the bead relative to the fixed XYZ coordinate system

$\vec v_{\text{bead/C}}$ = the velocity of the bead relative to a non-rotating reference frame moving with the center of the circular hoop

$\vec v_{C/XYZ}$ = the velocity of the center of the hoop with respect to the fixed XYZ coordinate system.

Is it because the direction of the tangential velocity is always changing? Thus, my equations will only be satisfied when the tangential velocities from both of them are parallel.

 

[TSny]

Is it because the direction of the tangential velocity is always changing? Thus, my equations will only be satisfied when the tangential velocities from both of them are parallel.

Even when the tangential velocities due to $\omega$ and $\dot \theta$ are parallel, your formula would not give the correct speed for the bead. When the bead is instantaneously at $\theta = 0$, the speed of the bead would be $a\dot \theta + 2a\omega$; whereas, your formula gives $a\dot \theta + a\omega$.

Note that if the bead is at rest with respect to the hoop and is located at the end of the diameter that passes through the origin (i.e., $\theta = 0$) the bead would have a speed of $2a\omega$ since the bead would be moving in a circle of radius $2a$ with angular speed $\omega$.

 

[Kelly Lin]

Even when the tangential velocities due to $\omega$ and $\dot \theta$ are parallel, your formula would not give the correct speed for the bead. When the bead is instantaneously at $\theta = 0$, the speed of the bead would be $a\dot \theta + 2a\omega$; whereas, your formula gives $a\dot \theta + a\omega$.

Note that if the bead is at rest with respect to the hoop and is located at the end of the diameter that passes through the origin (i.e., $\theta = 0$) the bead would have a speed of $2a\omega$ since the bead would be moving in a circle of radius $2a$ with angular speed $\omega$.

How about " the velocity of the bead relative to a non-rotating reference frame moving with the center of the circular hoop". The center of the circular hoop also rotates, so how can I find a non-rotating reference that is moving as the center of the circular hoop?
Sorry! I still don't get it! I still don't know how to use the relative velocity to solve this question.

 

[TSny]

how can I find a non-rotating reference that is moving as the center of the circular hoop?

In the figure above, the origin of the primed axes (blue) moves with the center of the hoop. But these axes do not rotate relative to the earth. The primed axes remain parallel to the unprimed axes as the hoop rotates.

The velocity of the bead relative to the Earth can be written as $$\vec v_{\text{bead/xyz}} = \vec v_{\text{bead/x'y'z'}} + \vec v_{C/\text{xyz}}$$ The first velocity on the right is the velocity of the bead relative to the primed axes and the second velocity vector on the right is the velocity of the center of the hoop relative to the unprimed axes. These velocity vectors are shown below in green and orange. The velocity of the bead relative to the Earth is the sum of these two vectors.

 

[Kelly Lin]

View attachment 208816

In the figure above, the origin of the primed axes (blue) moves with the center of the hoop. But these axes do not rotate relative to the earth. The primed axes remain parallel to the unprimed axes as the hoop rotates.

The velocity of the bead relative to the Earth can be written as $$\vec v_{\text{bead/xyz}} = \vec v_{\text{bead/x'y'z'}} + \vec v_{C/\text{xyz}}$$ The first velocity on the right is the velocity of the bead relative to the primed axes and the second velocity vector on the right is the velocity of the center of the hoop relative to the unprimed axes. These velocity vectors are shown below in green and orange. The velocity of the bead relative to the Earth is the sum of these two vectors.

View attachment 208819

Thank you very much for your diagrams!
I got it! The relative velocity of the bead is a(\dot{\theta}+\omega)!
Thanks again!

 

[TSny]

I got it! The relative velocity of the bead is a(\dot{\theta}+\omega)!

Yes. That's the magnitude.