godkills
- 42
- 0
Can someone tell me why there is no initial momentum when these 2 objects collide in the y direction?
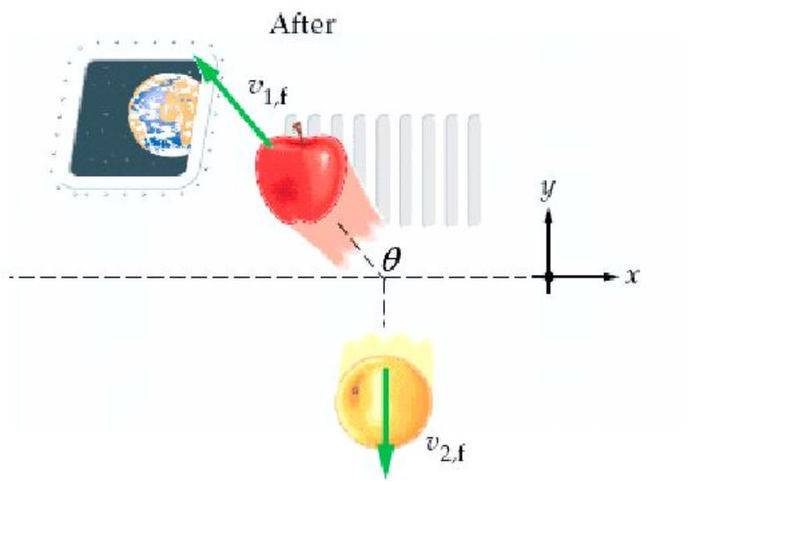
At first these objects were going in the x direction this picture shows what happens when the objects collided.
Apple Orange
=======> <========
that is what it would look like when the objects going in x direction
At first these objects were going in the x direction this picture shows what happens when the objects collided.
Apple Orange
=======> <========
that is what it would look like when the objects going in x direction