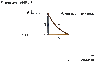- #1
as11
- 5
- 0
Problem:
One (1.00) mole of an ideal diatomic gas (with = 1.40) initially at 20.6°C and 1.00 atm pressure is taken around the following cycle:
Path (1): an isochoric increase in pressure until the temperature of the gas is 159°C and the pressure is P;
Path (2): an adiabatic expansion until the pressure returns to 1.00 atm;
Path (3): an isobaric compression until the gas reaches its original volume.
[[FIGURE ATTACHED]]
(a) What is the original volume of the gas at the beginning and end of the cycle?
(b) What is the pressure of the gas at the completion of path (1)?
(c) What is the volume of the gas at the completion of path (2)?
(d) What is the temperature of the gas at the completion of path (2)?
(e) Calculate the work done by the gas during each path of the cycle and the total work done by the gas.
1. (along path (1))
2. (along path (2))
3. (along path (3))
4. (total work)
(f) Calculate the heat transfer to the gas during each path of the cycle and the total heat transfer to the gas over the cycle.
1. (along path (1))
2. (along path (2))
3. (along path (3))
4. (total heat transfer)
(g) Find the efficiency of the cycle.
(h) Calculate the maximum efficiency that a heat engine could have if it operated between the hottest and coldest temperatures encountered by this gas in this cycle.
Attempt at a Solution:
**Let the point at the beginning of Path 1=a, end of path 1=b, end of path 2=c
a)V_{a}=\frac{nRT}{P} (where P=P_{a} and T=T_{a}) --->This gives the correct answer .0241 m^3
b)P_{b}=\frac{nRT}{V} --> V_{b}=V_{a}; this gives the correct answer 142149 Pa
c) P_{c}V^{\gamma}_{c}=P_{b}V^{\gamma}_{b} ----->this gives the correct answer .0307 m^3
d) T_{c}=\frac{P_{c}V_{c}}{nR} ----->this gives the correct answer 382 K.
...NOW, to where I'm having trouble.
e) 1. W=0 because \intPdV = W_{AB} ---->dv=0 this gives the correct answer
e2. W_{BC} = -\DeltaU +Q, adiabatic process--> Q=0, so W_{BC}=-\DeltaU
=-nC_{v}\DeltaT
=-1.00(20.8)(432K-382K) = -1040 but apparently this is wrong. I tried the positive value just to be safe, but that was incorrect as well.
e3. W_{CA}=\intPdV ---> pressure is constant, so
W_{CA}=P\DeltaV = (1.013 x 10^{5} Pa)(.0307-.0241) = 669, but I also tried the negative and both were incorrect.
e4. Just the sum of all e1+e2+e3, I assume
f) 1. Q=nC_{v}\DeltaT ---> this gives correct answer2879 J
f2. Q=0, adiabatic process-->correct answer
f3. Q= nC_{p}\DeltaT ---->this gives correct answer -2572 J
f4. First, I tried adding them all up, which was wrong, so I tried the negative, which was wrong and then realized it should be the opposite value of each number, which gave the wrong answer so I tried the negative of that, which was also wrong...
I got g (and I'm getting tired of using this formatting
) but if you want me to show how I did it just to see my thought process, I will. I'm assuming h shouldn't be hard either, once I have the correct values for everything.
THANK YOU FOR ANY HELP YOU CAN GIVE!
One (1.00) mole of an ideal diatomic gas (with = 1.40) initially at 20.6°C and 1.00 atm pressure is taken around the following cycle:
Path (1): an isochoric increase in pressure until the temperature of the gas is 159°C and the pressure is P;
Path (2): an adiabatic expansion until the pressure returns to 1.00 atm;
Path (3): an isobaric compression until the gas reaches its original volume.
[[FIGURE ATTACHED]]
(a) What is the original volume of the gas at the beginning and end of the cycle?
(b) What is the pressure of the gas at the completion of path (1)?
(c) What is the volume of the gas at the completion of path (2)?
(d) What is the temperature of the gas at the completion of path (2)?
(e) Calculate the work done by the gas during each path of the cycle and the total work done by the gas.
1. (along path (1))
2. (along path (2))
3. (along path (3))
4. (total work)
(f) Calculate the heat transfer to the gas during each path of the cycle and the total heat transfer to the gas over the cycle.
1. (along path (1))
2. (along path (2))
3. (along path (3))
4. (total heat transfer)
(g) Find the efficiency of the cycle.
(h) Calculate the maximum efficiency that a heat engine could have if it operated between the hottest and coldest temperatures encountered by this gas in this cycle.
Attempt at a Solution:
**Let the point at the beginning of Path 1=a, end of path 1=b, end of path 2=c
a)V_{a}=\frac{nRT}{P} (where P=P_{a} and T=T_{a}) --->This gives the correct answer .0241 m^3
b)P_{b}=\frac{nRT}{V} --> V_{b}=V_{a}; this gives the correct answer 142149 Pa
c) P_{c}V^{\gamma}_{c}=P_{b}V^{\gamma}_{b} ----->this gives the correct answer .0307 m^3
d) T_{c}=\frac{P_{c}V_{c}}{nR} ----->this gives the correct answer 382 K.
...NOW, to where I'm having trouble.
e) 1. W=0 because \intPdV = W_{AB} ---->dv=0 this gives the correct answer
e2. W_{BC} = -\DeltaU +Q, adiabatic process--> Q=0, so W_{BC}=-\DeltaU
=-nC_{v}\DeltaT
=-1.00(20.8)(432K-382K) = -1040 but apparently this is wrong. I tried the positive value just to be safe, but that was incorrect as well.
e3. W_{CA}=\intPdV ---> pressure is constant, so
W_{CA}=P\DeltaV = (1.013 x 10^{5} Pa)(.0307-.0241) = 669, but I also tried the negative and both were incorrect.
e4. Just the sum of all e1+e2+e3, I assume
f) 1. Q=nC_{v}\DeltaT ---> this gives correct answer2879 J
f2. Q=0, adiabatic process-->correct answer
f3. Q= nC_{p}\DeltaT ---->this gives correct answer -2572 J
f4. First, I tried adding them all up, which was wrong, so I tried the negative, which was wrong and then realized it should be the opposite value of each number, which gave the wrong answer so I tried the negative of that, which was also wrong...
I got g (and I'm getting tired of using this formatting
) but if you want me to show how I did it just to see my thought process, I will. I'm assuming h shouldn't be hard either, once I have the correct values for everything.THANK YOU FOR ANY HELP YOU CAN GIVE!
