jmmstr
- 7
- 0
Homework Statement
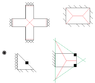
We were given many different slab sizes, shapes etc and asked to analyse them using Work = Energy equilibrium checks to find q, the maximum load per m^2 the slab can take.
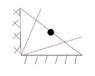
The first part was to show the fracture lines to use for analysis but I am stuck on one of them.
I have included the image below to show some examples of what I mean and the one I am stuck on.
Any help would be appreciated as always!
To clarify, the triangle one with the star above it is the one I am stuck on, the others I have shown working for.