- #1
sudera
- 25
- 0
- Homework Statement
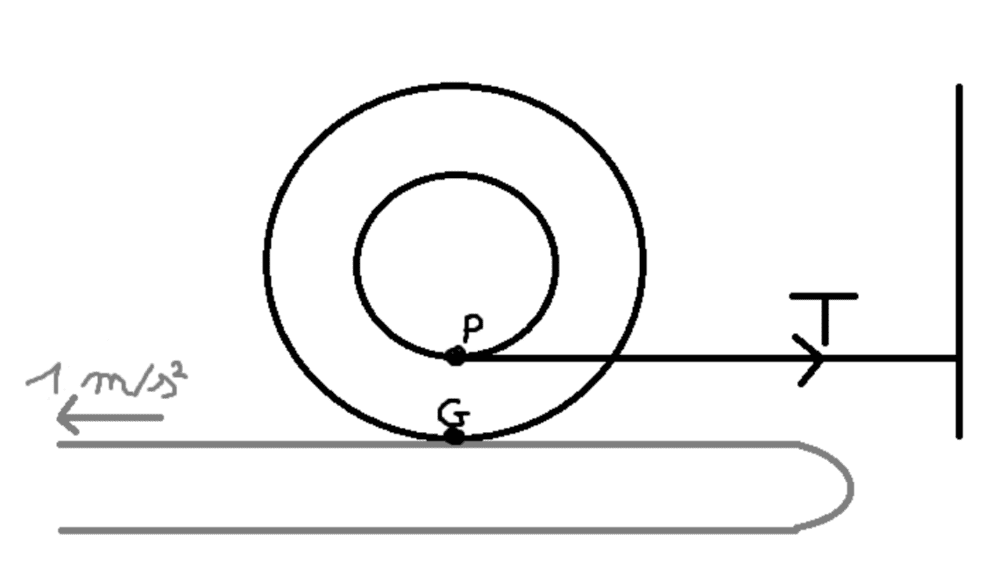
- A yo-yo is placed on a conveyor belt accelerating ##a_C = 1 m/s^2## to the left. The end of the rope of the yo-yo is fixed to a wall on the right. The moment of inertia is ##I = 200 kg \cdot m^2##. Its mass is ##m = 100kg##. The radius of the outer circle is ##R = 2m## and the radius of the inner circle is ##r = 1m##. The coefficient of static friction is ##0.4## and the coefficient of kinetic friction is ##0.3##.
Find the initial tension in the rope and the angular acceleration of the yo-yo.
- Relevant Equations
- ##T - f = ma##
##\tau_P = -fr##
##\tau_G = Tr##
##I_P = I + mr^2##
##I_G = I + mR^2##
##a = \alpha R##
First off, I was wondering if the acceleration of the conveyor belt can be considered a force. And I'm not exactly sure how to use Newton's second law if the object of the forces is itself on an accelerating surface.
Also, I don't know whether it rolls with or without slipping.
I thought I could use ##a_C = \alpha R## for the angular acceleration, but the acceleration of the conveyor belt is not the only source of acceleration, since the friction and the tension also play a role.
I can't find a way to combine these equations to get the
Also, I don't know whether it rolls with or without slipping.
I thought I could use ##a_C = \alpha R## for the angular acceleration, but the acceleration of the conveyor belt is not the only source of acceleration, since the friction and the tension also play a role.
I can't find a way to combine these equations to get the