TFM
- 1,016
- 0
Homework Statement
A hydrogen atom is interacting with an external magnetic field.
1. Derive the equation for the g_F-factor of the hyperfine states.
Homework Equations
The Attempt at a Solution
Okay, so the question asks to define the gF factor, however, I am not quite sure where to start.
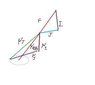
I know firstly that it is based on the diagram of the vector arrows, as (crudely drawn) attached:
I also know the answer I need to get (it is mentioned in the notes):
g_F = g_J\frac{F(F + 1) + j(j + 1) - I(I +1)}{2F(F + 1)} + \frac{\mu_N}{\mu_B}g_I \frac{F(F + 1) + I(I + 1) - j(j +1)}{2F(F + 1)}
Also, for the gJ, it starts with:
H_J = \frac{\mu_N}{\hbar}(\hat{L} + 2\vec{S})\cdot \vec{B} = \frac{\mu_N}{\hbar}(\hat{J} + \vec{S})\cdot \vec{B}
and I know for gF, we have:
H_J = \frac{\mu_B}{\hbar}(\hat{L} + 2\vec{S})\cdot \vec{B} - g_I ({\frac{\mu_N}{\hbar} \vec{I}\cdot \vec{B})
Anyone got any suggestions about what I should do first?
TFM