Calculating Cable Length and Stretch for Uniform Iron Beam in Static Equilibrium

[Juntao]

Picture is attached.

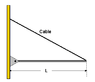
The above figure shows a uniform iron beam of mass 254 kg and length L = 3 m. The cable holding the beam in place can take a tension of 1300 N before it breaks. (You may ignore the small mass of the cable in this calculation.)

======
a)What minimum length of the cable?
b) Assume the cable is made of steel and has a diameter of 1". How much will it stretch before it breaks?

============
Okay. I am stuck on part a so far. I know that this is a static equilibrium, therefore, the summation of all the forces in x and y direction equal zero.
Also, the summation of torques must also equal zero.

But I'm not sure how to write out the equations. Can someone give me a lending hand?

 

[jamesrc]

Let me try to label some forces without drawing a picture:

The weight of the bar, W, acts at the center of mass of the bar (1.5 m from the left end (set your origin at the left end)).

The tension in the cable, T, has components T_x (clearly pointing to the left) and T_y (pointing up).

The mounting of the bar (pin joint) can support a vertical force, R_y (pointing up) and a horizontal force, R_x (pointing to the right).

Some equations for static equilibrium:

\Sigma F_y = R_y + T_y - W = 0

\Sigma F_x = R_x - T_x = 0

\Sigma M_o = T_y\cdot L - \frac{WL}{2} = 0

You can use these to find the y-component of the tension (actually, you only need the moment equation), but not much else.

Say you've solved for T_y and you want to find the minimum length of cable. You know that for the minimum length of cable, the cable tension will be at its maximum (not a great plan from an engineering standpoint, but nonetheless...). So:

T = \sqrt{T_x^2+T_y^2} = 1300

use that to solve for T_x.

The length of the cable is given by:

L_c = \frac{L}{\cos \theta}

where L_c is the length of the cable, L is the length of the bar (3 m), and θ is the angle between the cable and the bar, so that:

\tan\theta = \frac{T_y}{T_x}

That should allow you to find L_c

For part b, you should be able to use Hooke's law, σ = εE, to find the length it stretches (you have the tension, the cross sectional area, the unstretched length, and you can look up the Young's modulus).

 

[gnome]

I'm not sure as I haven't actually worked it through, but because both θ and L_c are unknown, you might also have to use
T_y = R_y

(This must be true since otherwise the bar would rotate about its center of mass.)