Solve Node Analysis Problem with Ideal Opamp

[svenneman]

Hi, I was searching google for answers about my problem and stumbled upon this forum. So I'll post my problem here and hope that some friendly soul can help me :)

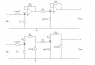
I need to do a node-analysis of the circuit that I've attached here. The opamp is ideal so Ri=inf and R0=0 and A=inf. I end up with 3 equations for the nodes v1,v2:
eq1: (1/(1/jwC1)+1/R1)v1 = Uin/(1/jwC1)
eq2: (1/R3 + 1/(1/jwC2))v2 = Av1/R3
eq3: Uout=Av2

I am pretty sure I've done wrong in the node analysis, but I am unable to find out what I've done wrong (or right ;)). The equations I get later by solving the equationsystems doesn't add up. Any input or help on this problem is greatly appreciated!

 

[SGT]

You did it wrong. Equation 1 should be:
U_{in}\dot(j\omega C_1 + \frac{1}{R_1}) = V_1\dot\frac{1}{R_1})
or, in simpler form:
V_1 = U_in\dot\frac{R_1}{R_1+\frac{1}{j\omegaC_1}
Since the amplifier is ideal, there is a virtual short circuit between the + and - terminals and the output voltage is V_1
Then equation 2 will be:
V_2 = V_1\dot\frac{\frac{1}{j\omegaC_2}}{R_2+\frac{1}{j\omegaC_2}
and
U_{out} = V_2

 

[SGT]

You did it wrong. Equation 1 should be:
U_{in}\dot(j\omega C_1 + \frac{1}{R_1}) = V_1\dot\frac{1}{R_1}
or, in simpler form:
V_1 = U_in\dot\frac{R_1}{R_1+\frac{1}{j\omegaC_1}}
Since the amplifier is ideal, there is a virtual short circuit between the + and - terminals and the output voltage is V_1
Then equation 2 will be:
V_2 = V_1\dot\frac{\frac{1}{j\omegaC_2}}{R_2+\frac{1}{j\omegaC_2}}
and
U_{out} = V_2

Reposted because I was not able to edit

 

[SGT]

Still unable to write correctly the equations in LaTex I will write it in normal text.
Eq.1: V1 = Uin [R1/(R1+1/jwC1)]
Eq.2: V2 = V1 [(1/jwC2)/(R2+1/jwC2)]

 

[svenneman]

Shouldnt it be R3 instead of R2 in your equations?

 

[SGT]

Shouldnt it be R3 instead of R2 in your equations?

Yes, my mistake.

 

[svenneman]

oky, then it makes more sense :P

thanks for the help, I'll sit down with the new equations and see if I can get a result out of it :)