Saladsamurai
- 3,009
- 7
Okay. I have been at this for two nights now. I want to derive, step by step, the equivalent spring constant of a Beam cantilevered at both ends with a loading at its center.
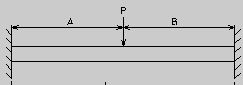
Here is a schematic with A=B=L/2
 Now I would like to use superposition to find the deflection at L/2 due to the loading. I know there are tables out there, but I want to "derive" this. (I know that I am not really deriving it since I am using superposition and tables...but bear with me).
Now I would like to use superposition to find the deflection at L/2 due to the loading. I know there are tables out there, but I want to "derive" this. (I know that I am not really deriving it since I am using superposition and tables...but bear with me).
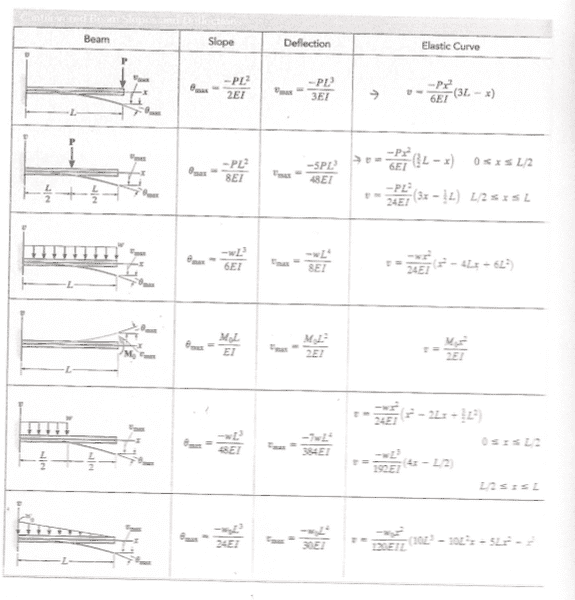
Here are the equations I have at my disposal. Calling them from top to bottom 1-6,
I think that 1, 2, and 4 will prove the most useful, but I could be wrong.
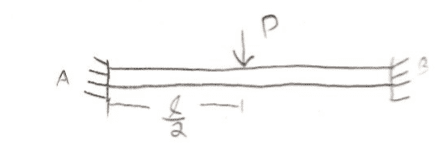
Now, if I replace the fixed end at the right with its reaction force and moment I have:
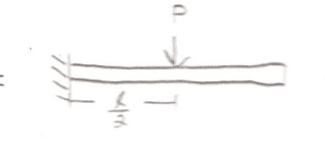
=
1
+
2

+
3

Here is a schematic with A=B=L/2
Here are the equations I have at my disposal. Calling them from top to bottom 1-6,
I think that 1, 2, and 4 will prove the most useful, but I could be wrong.
Now, if I replace the fixed end at the right with its reaction force and moment I have:
=
1
+
2
+
3
Last edited: