Differential limiting amplifier

[mmzaj]

HI

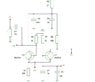
i know that the circuit attached to this thread is a differential limiting amplifier , and the collector of Q2 acts as a current source , but other than that , i can't get my mind around it ! P1 is the input , P5 is the output , and Vcc is +12 connected to the 27 R .

could someone please walk me step by step on how to analyze (understand) this freakin Amp !

 

[negitron]

Let's see if we can help you work this out on your own. First of all, can you determine what the state of the circuit is at quiescence (that is, with no input signal)? I'm assuming you're familiar with basic transistor theory, here.

 

[mmzaj]

well , here is a detailed DC analysis :

5=I_{B_{1}}R_{3}+V_{BE}+(\beta_{1}+1)R_{5}(I_{B_{1}}+I_{B_{2}})

and

5=I_{B_{1}}R_{4}+V_{BE}+(\beta_{2}+1)R_{5}(I_{B_{1}}+I_{B_{2}})

but because R_{3}=R_{4}=:R obviously :

I_{B_{1}}=I_{B_{2}}=:I_{B}

(( and \beta_{1}=\beta_{2}=:\beta assuming Q1 , Q2 are matched ))

and

5-0.7=(R+2(\beta+1)R_{5})I_{B}

hence

I_{B}=\frac{4.3}{R+2(\beta+1)R_{5}}

applying KVL to the outer loop :

12=2\beta R_{2}I_{B}+V_{CE_{1}}+2(\beta+1)I_{B}R_{5}

12=2\beta R_{2}I_{B}+V_{CE_{2}}+ \beta I_{B} R_{6}+2(\beta+1)I_{B}R_{5}

we have I_{b} , and we can find V_{CE_{1}},V_{CE_{2}} , and the rest of Is and Vs .

 

[negitron]

Nicely done.

Now, what happens to the output when you apply a signal which gradually increases in, say, +0.5 V increments to P2? We'll bypass P1 for now, since we just want to observe what happens at various instantaneous input voltage levels.

(I'll be off to bed now, so take your time!)

 

[mmzaj]

sadly , i don't have a scanner in order to upload my work , so i have to post it using latex , and man , it's sooo painful !

anyways , i'am not sure i got it right here , i neglected the effect of the capacitors , and didn't switch to AC small signal analysis !

let V @ P2 be V_{i}

then V_{i}=V_{BE_{1}}+(\beta +1)R_{5}(I_{B_{1}}+I_{B_{2}})

5=I_{B_{2}}R_{4}+V_{BE_{2}}+(\beta_{2}+1)R_{5}(I_{B_{1}} +I_{B_{2}})

=>5=I_{B_{2}}R_{4}+V_{i}

but 5=I_{B_{1}}R_{3}+V_{i}

=> I_{B_{1}}=I_{B_{2}}=:I_{B}

now

V_{CE_{2}}=12-(2\beta R_{2}+\beta R_{6}+2(\beta +1)R_{5})I_{B} = 12-\frac{(2\beta R_{2}+\beta R_{6}+2(\beta +1)R_{5})(5-V_{i})}{R_{3}}

let \frac{2\beta R_{2}+\beta R_{6}+2(\beta +1)R_{5}}{R_{3}}=:X

V_{E}=2(\beta +1)R_{5}I_{B}=\frac{2(\beta +1)R_{5}(5-V_{i})}{R_{3}}

let \frac{2(\beta +1)R_{5}}{R_{3}}=:Y

V_{C_{2}}=V_{E}+V_{CE_{2}}=12+(Y-X)(5-V_{i})

i don't have the data sheet of the 2N3904 - yet!- in order to obtain \beta , but clearly X>Y ... =>

V_{o} =V_{C_{2}}=A+gV_{i} where A is a DC offset , and g is some sort of a gain !

bare with me friend , i'am a detailed person !

 

[Bob S]

However, you need to look at the bias arrangements to see the real picture.
Those 1K resistors are very small and will hold the transistors deeply in saturation.

So, the small signal analysis doesn't really apply. This is a large signal circuit and will tend to poduce square wave output.

Not quite true. Both bases are approx the same voltage (but there should be a pot to balance small offsets). The voltage across R5 (820 ohms) is about 4.3 volts, so current is about 5.2 mA. This current is split between the two transistors equally. The voltage across R2 (27 ohms) is about 0.14 volts, and across R6 (820 ohms) is about 2.15 volts. So Q2 and by inference Q1 are both in the middle of their linear range. Good small signal amplifier.

 

[vk6kro]

Yes, sorry. I missed the 5V supply for the 1 Ks.