Rugile
- 79
- 1
Homework Statement
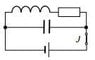
A source of ε = 10V, capacitor of C = 5 μf, inductor of L = 15 mH and r = 10 Ω and a resistor of R = 100 Ω are connected as in the schematic (attached). How much heat will dissipate in the resistor after the switch is opened?
Homework Equations
dQ = I2Rdt
KVL
The Attempt at a Solution
First of all I was quite confused by the question, so I just assumed that the switch is opened after a long time, when the capacitor and the inductor are fully charged. Then the voltage across the capacitor is U0 = ε and the current in the inductor is I0 = ε / (R+r). We can write the equation (KVL):
L\frac{dI}{dt} + I(R+r) + U_C = 0, where UC is the voltage across the capacitor. I get stuck here - I suppose I could write second order differential equation involving the function of q: L \frac{d^2 q}{dt^2} + (R+r) \frac{dq}{dt} + \frac{C}{q} = 0, but I'm not sure what to do with that either. Any hints?