Hilbert Definition and 293 Threads
-

Graduate Einstein Hilbert action, why varies wrt metric tensor?
The principle of least action states that the evolution of a physical system - how a system progresses from one state to another- is given by a stationary point of the action. So I think this is varying the path and keeping two points fixed- the points of the initial and final state I know...- binbagsss
- Thread
- Einstein Hilbert Metric Metric tensor Tensor
- Replies: 1
- Forum: Special and General Relativity
-

Graduate Eigenfunctions orthogonal in Hilbert space
Hello, I am having a question regarding how eigenfunctions are orthogonal in Hilbert space, or what does that even mean (other than the inner product is zero). I mean, I know in ##\mathbb {R^{3}}##, vectors are orthogonal when they are right angles to each other. However, how can functions be...- gfd43tg
- Thread
- Eigenfunctions Hilbert Hilbert space Orthogonal Space
- Replies: 4
- Forum: Quantum Physics
-
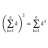
Graduate Hilbert space transformation under Poincaré translation
This is one of those "existential doubts" that most likely have a trivial solution which I can't see. Veltman says in the Diagrammatica book: Although the reasoning makes perfect sense for a Hilbert space spanned by momentum states, intuitively it doesn't make sense to me, because a...- ddd123
- Thread
- Hilbert Hilbert space Poincare Space Transformation Translation
- Replies: 3
- Forum: Quantum Physics
-
V
Graduate Why two-state system = two-dimensional Hilbert space?
When we talk about a two-state quantum system being a two-dimensional complex Hilbert space are we implicitly considering the "existence of time"? Why is all this additional structure (of a two-dimensional complex Hilbert space) necessary if, even with a full quantum mechanical perspective...- V0ODO0CH1LD
- Thread
- Hilbert Hilbert space Space System
- Replies: 2
- Forum: Quantum Physics
-

Graduate Rigged Hilbert Space Φ ⊂ H ⊂ Φ'
Hi, I am reading the paper http://arxiv.org/abs/quant-ph/0502053 listed in the reference of Wikipedia Rigged Hilbert Space. I have a question about the relation, Φ ⊂ H ⊂ Φ', where H is Hilbert space, Φ is its subspace and Φ' is dual space of Φ. Φ⊂H and Φ⊂Φ' are obvious. How can we say H ⊂...- sweet springs
- Thread
- Hilbert Hilbert space Space
- Replies: 61
- Forum: Quantum Physics
-

Graduate Question About Hilbert Space Convention
According to Wikipedia:http://en.wikipedia.org/wiki/Hilbert_space the inner product \langle x | y \rangle is linear in the first argument and anti-linear in the second argument. That is: \langle \lambda_1 x_1 + \lambda_2 x_2 | y \rangle = \lambda_1 \langle x_1 | y \rangle + \lambda_2 \langle...- stevendaryl
- Thread
- Convention Hilbert Hilbert space Space
- Replies: 5
- Forum: Quantum Physics
-
W
Graduate Special Properties of Hilbert Spaces?
Hi All, AFAIK, the key property that separates/differentiates a Hilbert Space H from your generic normed inner-product vector space is that , in H, the norm is generated by an inner-product, i.e., for every vector ##v##, we have## ||v||_H= <v,v>_H^{1/2} ##, and a generalized version of the...- WWGD
- Thread
- Hilbert Hilbert space Hilbert spaces Properties
- Replies: 33
- Forum: Topology and Analysis
-
M
Graduate Finding the Normal Cone of a Closed Convex Subset in a Hilbert Space
Let \text{ } H \text{ }be \text{ }a \text{ } Hilbert \text{ } space, \text{ }K \text{ }be \text{ }a \text{ }closed\text{ }convex\text{ }subset \text{ } of \text{ }H \text{ }and \text{ }x_{0}\in K. \text{ }Then \\N_{K}(x_{0}) =\{y\in K:\langle y,x-x_{0}\rangle \leq 0,\forall x\in K\} .\text{...- moh salem
- Thread
- Closed Cone Convex Hilbert Hilbert space Normal Space
- Replies: 5
- Forum: Topology and Analysis
-
K
Graduate Requirement of Separability of Hilbert Space
I have started reading formal definitions of Hilbert Spaces. I don't understand the requirement of separability postulate. I have proved that it leads to count ability of basis but again why is that required at first place.- Kushagra Nigam
- Thread
- Hilbert Hilbert space Space
- Replies: 17
- Forum: Quantum Physics
-
L
Graduate Operators on infinite-dimensional Hilbert space
Hello all! I have the following question with regards to quantum mechanics. If ##H## is a Hilbert space with a countably-infinite orthonormal basis ##\{ \left | n \right \rangle \}_{n \ \in \ \mathbb{N} }##, and two operators ##R## and ##L## on ##H## are defined by their action on the basis...- linbrits
- Thread
- Hilbert Hilbert space Operators Operators on hilbert space Space
- Replies: 3
- Forum: Quantum Physics
-
&
Graduate Canonical Commutation Relations in finite dimensional Hilbert Space?
So lately I've been thinking about whether or not it'd be possible to have the commutation relation [x,p]=i \hbar in a Hilbert Space of finite dimension d. Initially, I was trying to construct a lattice universe and a translation operator that takes a particle from one lattice point to the...- "pi"mp
- Thread
- Commutation Finite Hilbert Hilbert space Relations Space
- Replies: 10
- Forum: Quantum Physics
-

Graduate Separable Hilbert space's postulate
The first postulate of quantum mechanics says that every physical system is associated with a separable complex Hilbert space, however this does not hold for a free particle, where the basis is uncountable (all the momentum kets). I think it also does not hold for a free falling particle...- lfqm
- Thread
- Hilbert Separable
- Replies: 6
- Forum: Quantum Physics
-

Graduate Energy levels and Hilbert Spaces
Hi. Is there a Hilbert Space for each energy level of a system? (And, in general, for every point in time?) I read in some book that if a equation for a problem accepts two different sets of wavefunction solutions (the case in question was the free particle and the sets of solutions in...- carllacan
- Thread
- Energy Energy levels Hilbert Hilbert spaces Levels
- Replies: 4
- Forum: Quantum Physics
-
T
Graduate Question about wavefunctions and their Hilbert space
Maybe someone here can explain me something I never understood in QM: The wave function lives in the Hilbert space spanned by the measurement operator. Is there any mathematical relation of those spaces with each other?- Tosh5457
- Thread
- Hilbert Hilbert space Space Wavefunctions
- Replies: 8
- Forum: Quantum Physics
-

Graduate Dimensions of Hilbert Spaces confusion
If I understand it, Hilbert spaces can be finite (e.g., for spin of a particle), countably infinite (e.g., for a particle moving in space), or uncountably infinite (i.e., non-separable, e.g., QED). I am wondering about variations on this latter. The easiest uncountable to imagine is the...- nomadreid
- Thread
- Confusion Dimensions Hilbert Hilbert spaces
- Replies: 35
- Forum: Quantum Physics
-
S
Quantum Mechanics Book and resources on Hilbert Spaces
I am currently in a modern physics course and would to do more advanced study in quantum mechanics before taking the senior-level Quantum Mechanics course at my school. We use Townsend's modern physics book for the class that I am in right now; here is a link...- SheikYerbouti
- Thread
- Book Hilbert Hilbert spaces Mechanics Quantum Quantum mechanics Quantum mechanics book Resources
- Replies: 1
- Forum: Science and Math Textbooks
-
W
Graduate Bra and Ket Representation in Dual Hilbert Space
Hi, if ket is 2+3i , than its bra is 2-3i , my question is 2+3i is in Hilbert space than 2-3i can be represented in same hilbert space, but in books it is written we need dual Hilbert space for bra?- wasi-uz-zaman
- Thread
- Dual Hilbert Hilbert space Space
- Replies: 3
- Forum: Quantum Physics
-
C
Graduate Hilbert, Banach and Fourier theory
Hi. I want to get a quick overview of the theory of Hilbert spaces in order to understand Fourier series and transforms at a higher level. I have a couple of questions I hoped someone could help me with. - First of all: Can anyone recommend any literature, notes etc.. which go through the...- center o bass
- Thread
- Banach Fourier Hilbert Theory
- Replies: 3
- Forum: Linear and Abstract Algebra
-
S
Graduate Determining how to find the 2-d hilbert space from fusing ising anyons
Hello all, I'm working through the following paper on topological quantum computing. http://www.qip2010.ethz.ch/tutorialprogram/JiannisPachosLecture In particular I'm trying to derive and solve the pentagon equation in order to evaluate the F matrices for ising anyons. One thing I'm trying...- Shinn497
- Thread
- Hilbert Hilbert space Space
- Replies: 1
- Forum: Quantum Physics
-
A
Graduate Hilbert space, orthonormal basis
My book says that "the countability of the ONS in a hilbert space H entails that H can be represented as closure of the span of countably many elements". I must admit my english is probably not that good. At least the above quote does not make sense to me. What is it trying to say? Previously... -

Graduate What Distinguishes Hilbert Spaces from Euclidean Spaces?
I know that hilbert space is infinite dimension space whereas eucledian is Finite n dimensional space, but what are all other differences between them?- ajayguhan
- Thread
- Hilbert Space
- Replies: 30
- Forum: Linear and Abstract Algebra
-
A
Graduate Orthonormal system in Hilbert space
Let H be a Hilbert space. Let F be a subset of H. F is dense in H if: <f,h>=0 for all f in F => h=0 Now take an orthonormal set (ek) (this is a countable sequence indexed by k) in H. My book says that obviously: \bigcupspan(ek) is dense in H (the union runs over all k) => g=Ʃ<g,ek>ek Now... -
K
Spectrum of Momentum operator in the Hilbert Space L^2([-L,L])
Homework Statement Find the spectrum of the Momentum operator in the Hilbert Space defined by L^2([-L,L]), consisting of all square integrable functions ψ(x) in the range -L, to L Homework Equations We can get the resolvent set containting all λ in ℂ such that you can always find a...- krko
- Thread
- Hilbert Hilbert space Momentum Operator Space Spectrum
- Replies: 5
- Forum: Advanced Physics Homework Help
-
L
Graduate Do Hilbert Space Isomorphism Map Dense Sets to Dense Sets?
Suppose that H, K are Hilbert spaces, and A : H -> K is a bounded linear operator and an isomorphism. If X is a dense set in H, then is A(X) a dense set in K? Any references to texts would also be helpful.- logarithmic
- Thread
- Hilbert Hilbert space Isomorphism Map Sets Space
- Replies: 1
- Forum: Topology and Analysis
-
G
Graduate Given a Hamiltonian how do you pick the most convenient Hilbert space?
For example, I have a 3D particle that experiences a harmonic oscillator potential only in the X,Y plane for all Z ie. a free particle in the Z direction. This seems like cylindrical coordinates but I'm not sure how to express the Hilbert space if I want to be able to describe states and...- golnat
- Thread
- Hamiltonian Hilbert Hilbert space Space
- Replies: 3
- Forum: Quantum Physics
-
H
Dimension of Hilbert space (quantum mechanics)
Homework Statement Consider the states with the quantum numbers n = l = 1 and s = 1/2 Let J = L + S What is the dimension of the Hilbert space to describe all states with these quantum numbers? Homework Equations The Attempt at a Solution I believe the dimension of the Hilbert...- Haye
- Thread
- Dimension Hilbert Hilbert space Mechanics Quantum mechanics Space
- Replies: 4
- Forum: Advanced Physics Homework Help
-
A
Graduate The pure-point subspace of a Hilbert space is closed
(All that follows assumes we are talking about a self-adjoint operator A on a Hilbert space \mathscr H.) The first volume of Reed-Simon defines \mathscr H_{\rm pp} = \left\{ \psi \in \mathscr H: \mu_\psi \text{ is pure point} \right\}. The book seems to take for granted that \mathscr H_{\rm...- AxiomOfChoice
- Thread
- Closed Hilbert Hilbert space Space Subspace
- Replies: 3
- Forum: Topology and Analysis
-
L
Graduate Do bras and inner products relate in a Rigged Hilbert Space?
One of the most important results of functional analysis is that for every bounded linear functional f: H → ℂ on a Hilbert space H, there exists a fixed |v> in H such that f(|u>) is equal to the inner product of |v> with |u> for all |u> in H. This justifies the labeling of f as <v| in the...- lugita15
- Thread
- Hilbert Hilbert space Space
- Replies: 9
- Forum: Quantum Physics
-
P
Graduate A problem about non-separable Hilbert space
also see http://planetmath.org/exampleofnonseparablehilbertspace the main difficulty is about the completeness, which is hard to prove, the author's hint seems don't work here, for you can not use the monotone convergence theorem directly , f(x)χ[-N,N]/sqrt[N] is not monotone- prophetlmn
- Thread
- Hilbert Hilbert space Space
- Replies: 7
- Forum: Topology and Analysis
-
I
MHB Proving H is Complete & a Hilbert Space: Analysis of $\|.\|_H$
Hi, Let H = \{(x_n)_n \subseteq \mathbb{R} | \sum_{n=1}^{\infty} x_n < \infty \} and for $(x_n)_n \in H$ define $$\|(x_n)_n\|_H = \sup_{n} \left|\sum_{k=0}^{n} x_k \right|$$ Prove that $H$ is complete. Is $H$ a Hilbert space? What is the best way to prove $H$ is complete? To prove it's a...- Impo
- Thread
- Analysis Complete Hilbert Hilbert space Space
- Replies: 5
- Forum: Topology and Analysis
-
K
Graduate Hilbert Space in Quantum Mechanics
in quantum mechanics we have something called hilbert space. What does the dimensions of this space represent for that system? also is ψ(x) same as |ψ> in the dirac notation?- klen
- Thread
- Hilbert Hilbert space In quantum mechanics Mechanics Quantum Quantum mechanics Space
- Replies: 2
- Forum: Quantum Physics
-
Y
Graduate Tensor product of Hilbert spaces
Hi everyone, I don't quite understand how tensor products of Hilbert spaces are formed. What I get so far is that from two Hilbert spaces \mathscr{H}_1 and \mathscr{H}_2 a tensor product H_1 \otimes H_2 is formed by considering the Hilbert spaces as just vector spaces H_1 and H_2...- Yoran91
- Thread
- Hilbert Hilbert spaces Product Tensor Tensor product
- Replies: 6
- Forum: Linear and Abstract Algebra
-
C
Graduate Finite Hilbert Space v.s Infinite Hilbert Space in Perturbation Theory
Hi all, I have a question about the concept of complete set when I apply the perturbation theory in two situations -Finite Hilbert Space and Infinite Hilbert Space. Consider a Hamiltonian H=H0+H', where H0 is the unperturbed Hamiltonian and H' is the perturbed Hamiltonian. Let ψ_n be the...- ck00
- Thread
- Finite Hilbert Hilbert space Infinite Perturbation Perturbation theory Space Theory
- Replies: 7
- Forum: Quantum Physics
-
M
Graduate Dimension of Rays in Hilbert Space
I am wondering, what is the dimension of a ray in a Hilbert space? For example here (page 2, bottom of page) I have read: I understand why a state is represented by all multiples of a vector, not just the vector. But is the ray really one-dimensional? It would be one-dimensional if we multiply...- mpv_plate
- Thread
- Hilbert Hilbert space Rays Space
- Replies: 5
- Forum: Quantum Physics
-
B
Verifying Inner Product & Showing $\ell^{2}$ is a Hilbert Space
Homework Statement let \ell^{2} denote the space of sequences of real numbers \left\{a_{n}\right\}^{\infty}_{1} such that \sum_{1 \leq n < \infty } a_{n}^{2} < \infty a) Verify that \left\langle \left\{a_{n}\right\}^{\infty}_{1}, \left\{b_{n}\right\}^{\infty}_{1} \right\rangle =...- BrainHurts
- Thread
- Hilbert Hilbert space Inner product Product Space
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
B
Graduate What Challenges Arise in QM/QFT with Non-Separable Hilbert Spaces?
What goes wrong if you try to do QM/QFT with a non-separable Hilbert space? Why do the Wightman axioms stipulate a separable space? And I need something else cleared up: The Hilbert space of non-trivial QFTs are indeed non-separable right?- Bobhawke
- Thread
- Hilbert Hilbert spaces
- Replies: 12
- Forum: Quantum Physics
-

Show that a vector space is not complete (therefore not a Hilbert spac
Homework Statement Consider the space of continuous functions in [0,1] (that is C([0,1]) over the complex numbers with the following scalar product: ##\langle f , g \rangle = \int _0 ^1 \overline{f(x)}g(x)dx##. Show that this space is not complete and therefore is not a Hilbert space. Hint:Find...- fluidistic
- Thread
- Complete Hilbert Space Vector Vector space
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
J
Graduate What good are rigged hilbert spaces?
I have seen the definition of a rigged Hilbert space many times, but I have never seen rigged Hilbert spaces actually being used for anything. Like for proving something. Has anyone else ever seen rigged Hilbert spaces being used for proving something?- jostpuur
- Thread
- Hilbert Hilbert spaces
- Replies: 8
- Forum: Topology and Analysis
-
T
Graduate Hilbert Space Interpretation of Fourier Transform
I've been taught (in the context of Sturm-Liouville problems) that Fourier series can be explained using inner products and the idea of projection onto eigenfunctions in a Hilbert space. In those cases, the eigenvalues are infinite, but discrete. I'm now taking a quantum mechanics course, and...- thegreenlaser
- Thread
- Fourier Fourier transform Hilbert Hilbert space Interpretation Space Transform
- Replies: 16
- Forum: Linear and Abstract Algebra
-
P
Graduate Composite system, rigged Hilbert space, bounded unbounded operator, CSCO, domain
Is something wrong in my assertions below? Suppose we have two quantum systems N and X. Let N is described by discrete observable \hat{n} (bounded s.a. operator with discrete infinite spectrum) with eigenvectors |n\rangle. Let X is described by continuous observable \hat{x} (unbounded s.a...- Petro z sela
- Thread
- Bounded Composite Domain Hilbert Hilbert space Operator Space System
- Replies: 3
- Forum: Quantum Physics
-
P
Graduate Rigged Hilbert space, separable space, domain of CSCO, mapping
Suppose that we have rigged Gilbert space Ω\subsetH\subsetΩ\times (H is infinite-dimensional and separable). Is the Ω a separable space? Is the Ω\times a separable space? Consider the complete set of commuting observables (CSCO) which contain both bounded and unbounded operators...- Petro z sela
- Thread
- Domain Hilbert Hilbert space Mapping Separable Space
- Replies: 29
- Forum: Quantum Physics
-

Methods of Mathematical Physics by Hilbert and Courant
Author: Richard Courant, David Hilbert Title: Methods of Mathematical Physics Amazon Link: https://www.amazon.com/dp/0471504475/?tag=pfamazon01-20 https://www.amazon.com/dp/0471504394/?tag=pfamazon01-20 Table of Contents for Volume I: The Algebra of Linear Transformations and Quadratic...- micromass
- Thread
- Hilbert Mathematical Mathematical physics Physics
- Replies: 1
- Forum: Science and Math Textbooks
-
H
Computing the Hilbert transform via Fourier transform
I know the result: \widehat{H(f)}=i\textrm{sgn}\hspace{1mm}(k)\hat{f} I thought I could use fft, and ifft to compute the transform easily, is there a MATLAB command for sgn? Mat- hunt_mat
- Thread
- Computing Fourier Fourier transform Hilbert Hilbert transform Transform
- Replies: 2
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
C
Graduate Problem with changing basis in Hilbert space
The expansion theorem in quantum mechanics states that a general state of a system can be represented by a unique linear combination of the eigenstates of any Hermitian operator. If that's the case then that would imply we would be able to represent the spin state of a particle in terms of...- Chain
- Thread
- Basis Hilbert Hilbert space Space
- Replies: 4
- Forum: Quantum Physics
-
E
Graduate On the domain of the function that undergoes the Hilbert transform
Hi all, This question is on the Hilbert transform, particularly on the domain of the input and output functions of the Hilbert transform. Before rising the question, consider the Fourier transform. The input is f(t) and the output is F(\omega). The function f and F are defined over...- elgen
- Thread
- Domain Function Hilbert Hilbert transform Transform
- Replies: 2
- Forum: Differential Equations
-

Problem in Logic - Hilbert Systems
Homework Statement In a Hilbert System, prove: \phi[x|m] \rightarrow\forall y((y=m)\rightarrow\phi[x|y]) where \phi is a formula, y, x are variables and m is a constant. \phi[a|b] denotes the formula obtained by substituting b for a in \phi This problem crops up in my attempting to prove...- andrewkirk
- Thread
- Hilbert Logic Systems
- Replies: 0
- Forum: Calculus and Beyond Homework Help
-
C
How Does Trace Class Operator Q Relate to Norms in Hilbert Spaces?
Hello, I'm reading Gaussian measures on Hilbert spaces by S. Maniglia (available via google) and I have the following issue, regarding the proof. He states in Lemma 1.1.4: Let μ be a finite Borel measure on H. Then the following assertions are equivalent: (1) \int_H |x|^2 \mu(dx) < \infty (2)...- camillio
- Thread
- Hilbert Hilbert space Norm Space
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
K
Proving the Norm of a Hilbert Space: Tips and Tricks for Success
Homework Statement Let H be a Hilbert space. Prove \Vert x \Vert = \sup_{0\neq y\in H}\frac{\vert (x,y) \vert}{\Vert y \Vert} The Attempt at a Solution First suppose x = 0. Then we have \sup_{0\neq y\in H}\frac{\vert (x,y) \vert}{\Vert y \Vert} = \sup_{0\neq y\in H}\frac{\vert (0,y)...- Kindayr
- Thread
- Hilbert Hilbert spaces
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
C
Can unitary operators on hilbert space behaive like rotations?
Homework Statement unitary operators on hilbert space Homework Equations is there a unitary operator on a (finite or infinite) Hilbert space so that cU(x)=y, for some constant (real or complex), where x and y are fixed non-zero elements in H ? The Attempt at a Solution I know the...- cyeus
- Thread
- Hilbert Hilbert space Operators Rotations Space
- Replies: 1
- Forum: Advanced Physics Homework Help
-
B
Graduate Equivalent vectors in a Hilbert space
In Griffith's intro to QM it says on page 95 (in footnote 6) : "In Hilbert space two functions that have the same square integral are considered equivalent. Technically, vectors in Hilbert space represent equivalence classes of functions." But that means that if we take for example...- bob900
- Thread
- Equivalent Hilbert Hilbert space Space Vectors
- Replies: 6
- Forum: Quantum Physics