Integrals Definition and 1000 Threads

In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus, and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others.
The integrals enumerated here are those termed definite integrals, which can be interpreted formally as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an antiderivative, a function whose derivative is the given function. In this case, they are called indefinite integrals. The fundamental theorem of calculus relates definite integrals with differentiation and provides a method to compute the definite integral of a function when its antiderivative is known.
Although methods of calculating areas and volumes dated from ancient Greek mathematics, the principles of integration were formulated independently by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century, who thought of the area under a curve as an infinite sum of rectangles of infinitesimal width. Bernhard Riemann later gave a rigorous definition of integrals, which is based on a limiting procedure that approximates the area of a curvilinear region by breaking the region into thin vertical slabs.
Integrals may be generalized depending on the type of the function as well as the domain over which the integration is performed. For example, a line integral is defined for functions of two or more variables, and the interval of integration is replaced by a curve connecting the two endpoints of the interval. In a surface integral, the curve is replaced by a piece of a surface in three-dimensional space.

View More On Wikipedia.org
Recent contents Top users
  1. chwala

    Evaluate the given integrals - line integrals

    My interest is on question ##37##. Highlighted in Red. For part (a) I have the following lines; ##\int_c A. dr = 4t(2t+3) +2t^5 + 3t^2(t^4-2t^2) dt ## ##\left[\dfrac {8t^3}{3}+ 6t^2+\dfrac{t^6}{3} + \dfrac{3t^7}{7} - \dfrac{6t^5}{5}\right]_0^1## ##=\dfrac{288}{35}## For part (b) for...
  2. P

    I On convolution theorem of Laplace transform: Schiff

    Here follows the theorem and proof: Questions: 1. I do not understand the following part "...and hence, in view of the preceding calculation, ##\int_0^\infty \int_0^\infty |e^{-st}f(\tau)g(t-\tau)|dtd\tau## converges". We know that ##\mathcal{L}\big(f(t)\big)## and...
  3. DifferentialGalois

    Exploring Shock Waves: A Mathematical Analysis

    the attempted is the above ex. i needa justify why and figure out the reason behind those relevant equations.
  4. C

    A Calculating the optical depth of an inhomogeous gas

    My question emerges from my desire to calculate the optical depth, which should be unitless, for an inhomgeneous cloud of radius ##r##. For a homogeneous medium, the optical depth can be defined in terms of the density of a cloud relative to the density of the condensed medium: $$\tau = \alpha...
  5. ananonanunes

    Find volume of this object using integrals

    I am given this expression which represents an object in 3D and the goal is to determine its volume using multiple integrals. I started by drawing what I think is the object as well as two "slices" of that object on different planes (z=2 and z=1) I have tried using cartesian, cylindrical and...
  6. George Wu

    A Do Time-ordering and Time Integrals commute? Peskin(4.22)(4.31)(4.44)

    In Peskin P85: It says the Time-ordered exponential is just a notation，in my understanding, it means $$\begin{aligned} &T\left\{ \exp \left[ -i\int_{t_0}^t{d}t^{\prime}H_I\left( t^{\prime} \right) \right] \right\}\\ &\ne T\left\{ 1+(-i)\int_{t_0}^t{d}t_1H_I\left( t_1 \right)...
  7. T

    A Non solvable integral? (dx/dt)^2 dt

    The integral is (dx/dt)^2 dt, where x=x(t) so it can't be just x + C. The non linear system for whom wants to know how did I get to that point is: d(dx/dt)/dt = sqrt(a^2+b^2)*sin(x+alfa+phi) - Kd*(dx/dt); where alfa = atan(a/b), phi = constant angle, Kd = constant coefficient. After...
  8. A

    Centroid calculation using integrals

    Hello! Im given this function ## f:[-\pi/2,1] -> [0,1]## with f(x) = 1-x for x (0,1] and f(x) = cos(x) for x ##[-\pi/2,0] ## And im susposed to find the centroid of this function so xs and ys. For that I am given these 2 equations ( I found them in the notes) ## x_s =\frac{1}{A}...
  9. mcastillo356

    I The Basic Area Problem (introduction to the topic of integrals)

    Hi PF There goes the quote: The Basic Area Problem In this section we are going to consider how to find the area of the region ##R## lying under the graph ##y=f(x)## of a nonnegative-valued, continous function ##f##, above the ##x##-axis and between the vertical lines ##x=a## and ##x=b##, where...
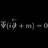
  10. qft-El

    A Heisenberg picture and Path integrals (Zee QFT)

    Reading the introduction to path integrals given in the latest edition of Zee's "Quantum field theory in a nutshell", I have found a remark which I don't really understand. The author is evaluating the free particle propagator ##K(q_f, t; q_i, 0)## $$\langle q_f\lvert e^{-iHt}\lvert q_i...
  11. Euge

    POTW Gaussian Integrals in Two Dimensions

    Let ##a, b##, and ##c## be real numbers such that ##a## and ##c## are positive and ##ac > b^2##. Evaluate the double integral $$\int_{-\infty}^\infty \int_{-\infty}^\infty e^{-ax^2 - 2bxy - cy^2}\, dx\, dy$$
  12. mncyapntsi

    Confused about polar integrals and setting up bounds

    So I want to subtract the two surfaces, right? I really don't know where to start... I am guessing this would be some sort of triple integral, however I am very confused with the bounds. Any help would be greatly appreciated! Thanks!!
  13. WMDhamnekar

    Line integrals and Stokes' theorem

    My answer:
  14. Euge

    POTW Exponential-Type Integrals

    Evaluate, with proof, the definite integral $$\int_{-\infty}^\infty \frac{e^{ax}}{1 + e^x}\, dx$$ where ##0 < a < 1##.
  15. P

    A Approximating integrals of Bessel functions

    I edited this to remove some details/attempts that I no longer think are correct or helpful. But my core issue is I have never seen this approach to approximating integrals that is used in the attached textbook image. Any more details on what is happening here, or advice on where to learn more...
  16. yucheng

    I Why are there 2s -1 independent integrals of motion?

    I was reading Mechanics by Landau and Lifshitz and I am confused when it is stated in chapter 2 section 6 that one of the integrals of motion is not independent and it can be considered an additive constant of time. Hence I tried searching it up online...
  17. WMDhamnekar

    I Properties of Line Integrals question

    I don't have any idea to answer these questions. I am working on it by searching the reference books where similar questions have been solved by authors. Meanwhile, any member of Physics Forums may help me in answering these questions.
  18. LCSphysicist

    Statistical mechanics and problem with integrals

    So we have a system of N non interacting particles, on a d-dimensional space, the system is in contact with a bath of temperature T. The hamiltonian is $$H = \sum_{l = 1}^{N} (A_{l}|p_{l}|^{s}+B_{l}|q_{l}|^{s})$$. What is the avarage energy? Now, i have some problems with statistical...
  19. WMDhamnekar

    Using Multiple integrals to compute expected value

    I want to know how did author derive the red underlined term in the following Example?
  20. yucheng

    I Do volume integrals involve bounding surfaces?

    In Vanderlinde page 171-172, the author derives the vector potential for the magnetic dipole (and free currents) \begin{align} \vec{A}(\vec{r}) &=\frac{\mu_{0}}{4 \pi} \int_{\tau} \frac{\vec{J}\left(\vec{r}^{\prime}\right) d^{3}...
  21. benorin

    I I need integrals Int[0,infty]t^(a-1) e^(-t) F(z, e^(-t))dt

    I’m doing some brainstorming for a note I’m writing, I would appreciate it if anybody knows interesting integrals of the form $$\int_{t=0}^\infty t^{\alpha - 1} e^{-t} F(z, e^{-t})\, dt=G( z, \alpha )$$ where ##z## and ##\alpha## are complex parameters and the solution ##G(z, \alpha )## is...
  22. WMDhamnekar

    Change of variables in multiple integrals

    Summary: Find the volume V of the solid inside both ## x^2 + y^2 + z^2 =4## and ## x^2 +y^2 =1## My attempt to answer this question: given ## x^2 + y^2 +z^2 =4; x^2 + y^2 =1 \therefore z^2 =3 \Rightarrow z=\sqrt{3}## ## \displaystyle\iiint\limits_R 1dV =...
  23. benorin

    Can Wolfram Alpha do n-d integrals symbolically?

    The Q is all in the title. I’ve been working on Selberg integrals, curious if Alpha can help me?
  24. Sophrosyne

    I Question about Feynman’s path integrals

    In Feynman’s path integrals, there is: ∫dq″Π0(t″,t′;q″,q′)=1 What is the funny pi looking symbol?
  25. WMDhamnekar

    Change in the order of integration in triple integrals

    If we solve the L.H.S. of this equation, we get ## \frac{(b-a)^3}{6}## and if we solve R.H.S. of this equation, we get ##-\frac{2b^3-3ba^2 +a^3}{6}## So, how can we say, this equation is valid? By the way, how can we use the hint given by the author here?
  26. WMDhamnekar

    MHB Triple Integrals: Finding Volume of Solid S Bounded by Planes

    Find the volume V of the solid S bounded by the three coordinate planes, bounded above by the plane x + y + z = 2, and bounded below by the z = x + y. How to answer this question using triple integrals? How to draw sketch of this problem here ?
  27. benorin

    I Looking for an expert on integrals

    I’ve written an insight article on what I think is original material (at least I’ve not seen it in my reading nor google): A Novel Technique of Calculating Unit Hypercube Integrals I am looking first for someone that can follow my work, I’ve had some mathematicians look over it but none whose...
  28. A

    A Multiplying divergent integrals using Hardy fields approach

    I wonder if the following makes sense. Suppose we want to multiply ##\int_0^\infty e^x dx\cdot\int_0^\infty e^x dx##. The partial sums of these improper integrals are ##\int_0^x e^x dx=e^x-1##. Now we multiply the germs at infinity of these partial sums: ##(e^x-1)(e^x-1)=-2 e^x+e^{2 x}+1##...
  29. Physics Slayer

    Integrals that keep me up at night

    Been struggling with a few integrals, I might post a few more once I progress further in my assignment. $$1. \int \sqrt{tanx} + \sqrt{cotx} (dx)$$ Attempt1: for integral 1, I try to apply integration by parts on both ##\sqrt{tanx}## and ##\sqrt{cotx}## separately, I then get $$\int...
  30. benorin

    Insights A Novel Technique of Calculating Unit Hypercube Integrals

    Introduction Best viewed on a desktop, if you must use a phone, maximize your browser in landscape mode and sorry some of the math won’t fully display on a mobile yet. In this insight article, we will build all the machinery necessary to evaluate unit hypercube integrals by a novel technique...
  31. D

    I Inverting an Equation Containing Elliptic Integrals

    Hello, For my own amusement, I am deriving the eqations for various roulettes, i.e. a the trace of a curve rolling on another curve. When considering rolling ellipses, I encounter equations containing elliptic integrals (of the second kind) that need to be inverted. For example, here is one...
  32. penguin46

    How to find integrals of motion for a particle on a surface?

    I have no idea where to even start with this, please help. I barely even know what integral of motion means.
  33. C

    Prove limit comparison test for Integrals

    Attempt: Note we must have that ## f>0 ## and ## g>0 ## from some place or ## f<0 ## and ## g<0 ## from some place or ## g ,f ## have the same sign in ## [ 1, +\infty) ##. Otherwise, we'd have that there are infinitely many ##x's ## where ##g,f ## differ and sign so we can chose a...
  34. U

    Engineering Path integrals in scalar fields when the path is not provided

    I cannot seem to start answering the question as a result of the path not being provided. How do I solve this when the path is not provided? See picture below
  35. dRic2

    I Stokes' theorem and surface integrals

    Hi, So my goal is to compute the integral of the "curl" of the vector field ##A_i(x_i)## over a 2-dimensional surface. Following a physics book that I am reading, I introduce the antisymmetric 2-nd rank tensor ##\Omega_{ij}##, defined as: $$\Omega_{ij} = \frac {\partial A_i}{\partial x_j} -...
  36. George Keeling

    I How do a bunch of integrals make an n-simplex or an n-cube?

    This question arises from Carroll's Appendix I on the parallel propagator where he shows that, in matrix notation, it is given...
  37. S

    Intro Physics Books for high school physics E&M [No integrals]

    Can you recommend introductory physics book for high school that contains E & M ? It should not have any integrals.
  38. DaalChawal

    MHB Shortcuts for Solving Multiple Integrals: Is There a Faster Way?

    I'm having a problem solving this, My approach is solving $x_1$ as a variable and rest as constants first and then going on further. But it is getting too lengthy. Is there any short method?
  39. MNaydenov

    Mathematica Loop integrals using Package-X 2.0 in Wolfram Mathematica

    Hello everyone, I have trouble installing Package-X 2.0 to Wolfram Mathematica. It says that the package should be available at https://packagex.hepforge.org but this page does not open. I tried everything I could to install and load this package but it was all unsuccessful. It seems as the...
  40. JD_PM

    Checking convergence of Gaussian integrals

    a) First off, I computed the integral \begin{align*} Z(\lambda) &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} dx \exp\left( -\frac{x^2}{2!}-\frac{\lambda}{4!}x^4\right) \\ &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} dx \exp\left( -\frac{x^2}{2!}\right) \exp\left(...
  41. A

    A Why physicists cannot renormalize all divergent integrals?

    Why the physicists have troubles with infinities in many physical theories, such as quantum gravity? Why cannot they just use divergent integrals and regularize or renormalize them in the end so to obtain finite values? I mean, operations on divergent integrals are not a problem, and techniques...
  42. M

    MHB Do These Integrals Converge or Diverge?

    Hey! :giggle: I want to check if the following integrals converge or diverge. 1 . $\displaystyle{\int_0^{+\infty}t^2e^{-t^2}\, dt}$ 2. $\displaystyle{\int_e^{+\infty}\frac{1}{t^n\ln t}\, dt, \ n\in \{1,2\}}$ 3. $\displaystyle{\int_0^{+\infty}\frac{\sin t}{\sqrt{t}}\, dt}$ 4...
  43. M

    Path Integrals in Wolfram Mathematica

    Hello everyone ! I am new to this site so I 'd better say hello to you all ! I am finishing my BR in physics and part of this ending is to deliver a thesis . Long story short I must compute path-integrals in SU(2) and SU(3) pure yang-mills fields . Problem is that i was never very good with...
  44. L

    A Elliptic Integral: Why Is It Called That?

    Why this integral is called elliptic? I(k)=\int^{\frac{\pi}{2}}_0(1-k^2\sin^2 \varphi)^{-\frac{1}{2}}d \varphi
  45. C

    Showing that these two integrals are equal

    Mentor note: The OP has been notified that more of an effort must be shown in future posts. These two are equal to each other, but I can't figure out how they can be that. I know that 2 can be taken out if its in the function, but where does the 2 come from here?
  46. D

    I Double integrals - do areas cancel?

    If i do a double integral of 1.dxdy to find an area of an odd function eg. y=x from +a to -a i get zero because the area below the x-axis cancels with the area above the x-axis. If i do a double integral of a circle centred at the origin i get the area to be πr2 ; so why doesn't the area below...
  47. E

    MHB Can double integrals be interpreted as net change?

    I understand that single integrals over a function can be interpreted as net change. Net change of the quantity between the bounds of the integration. But I am trying hard to understand if double integration can also be regarded as net change? That is, the net change in volume when the two input...
  48. E

    B Orientation of double integrals

    I learned that, because ##du \, dv = \frac{\partial(u,v)}{\partial(x,y)} dx \, dy##, if you set ##u=y## and ##v=x## then you get that ##dx \, dy = - dy \, dx##. And that the product of two differentials is a wedge product, which is antisymmetric. If coordinates are orthogonal, then ##dx \, dy =...
  49. K

    Calculating Curve Integrals with the Del Operator: A Pain in the Brain?

    My attempt is below. Could somebody please check if everything is correct? Thanks in advance!
  50. I

    I Confirming my knowledge on surface integrals

    Hi, I want to make sure my understanding of calculating surface integrals of vector fields is accurate. It was never presented this way in a textbook, but I put this together from pieces of knowledge. To my understanding, surface integrals can be calculated in four different ways (depending on...
Back
Top