Random Definition and 996 Threads
-

Graduate 2D space and 1D time evolution of a random field
I want to develop a 2D random field and its change with time with constant velocity. My process: 1. Define a 2D grid [x, y] with n \times n points 2. Define 1D time axis [t] with n_t elements 3. Find the lagrangian distance between the points in space with the velocity in x and y ...- tworitdash
- Thread
- 1d 2d Evolution Field Random Random number Random variable Space Time Time evolution
- Replies: 5
- Forum: Set Theory, Logic, Probability, Statistics
-

Random variable and probability density function
Hi, I was trying to solve the attached problem which shows its solution as well. I cannot understand how and where they are getting the equations 3.69 and 3.69A from. Are they substituting the values of θ₁ and θ₂ into Expression 1 after performing the differentiation to get equations 3.70 and...- PainterGuy
- Thread
- Density Density function Function Probability Probability density Probability density function Random Random variable Variable
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-

Undergrad Distribution function and random variable
Hi, I cannot figure out how they got Table 2.1. For example, how come when x=1, F_X(x)=1/2? Could you please help me with it? Hi-resolution copy of the image: https://imagizer.imageshack.com/img923/2951/w9yTCQ.jpg- PainterGuy
- Thread
- Distribution Distribution function Function Random Random variable Variable
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
F
Is gene replacement a practical way to fix random mutations?
Recently I asked if prime editing can be used to reverse the random mutations we accumulate with aging(https://www.physicsforums.com/threads/can-prime-editing-fix-every-harmful-mutation-in-all-our-cells.1003279/) but now I have a different question. Can we simply replace our genes to get rid of...- FTM1000
- Thread
- Gene Practical Random
- Replies: 10
- Forum: Biology and Medical
-
M
Variance of a point chosen at random on the circumference of a circle
Hi, I was looking at this problem and just having a go at it. Question: Let us randomly generate points ##(x,y)## on the circumference of a circle (two dimensions). (a) What is ##\text{Var}(x)##? (b) What if you randomly generate points on the surface of a sphere instead? Attempt: In terms of...- Master1022
- Thread
- Circle Circumference Point Probability Random Variance
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
M
Bound correlation coefficient for three random variables
Hi, I just found this problem and was wondering how I might go about approaching the solution. Question: Given three random variables ## X##, ##Y##, and ## Z ## such that ##\text{corr}(X, Y) = \text{corr}(Y, Z) = \text{corr}(Z, X) = r ##, provide an upper and lower bound on ##r## Attempt: I...- Master1022
- Thread
- Bound Coefficient Correlation Random Random variables Variables
- Replies: 3
- Forum: Precalculus Mathematics Homework Help
-
A
High School Is quantum coherence a random event?
How we should understand the randomness of quantum events in the context of the significant role that they apparently play in our macroscopic world. Using processes as superconductivity, super-fluidity, and in Bose-Einstein Condensates researchers have been able to produce macroscopic quantum...- arnell7
- Thread
- Coherence Quantum Quantum coherence Random
- Replies: 23
- Forum: Quantum Physics
-
T
Undergrad Do you have an example of a truly random phenomenon?
I tried to think of a truly random phenomena thatis not related to quantum physics, and i can't. Let's take heads or tails as an example, if you had all of the data about the throwing of the coin you could tell on which side it will land. So does anyone know a random phenomena?- The_Baron
- Thread
- Example Phenomenon Random
- Replies: 122
- Forum: Other Physics Topics
-
C
Undergrad Implementation of Correlated Gaussian Random Fields Model
Hello everyone. I have been recently working in an optimization model in the presence of uncertainty. I have read https://www.researchgate.net/publication/310742108_Efficient_Simulation_of_Stationary_Multivariate_Gaussian_Random_Fields_with_Given_Cross-Covariance in which, a methodology for...- confused_engineer
- Thread
- Articles Code Example Fields Gauss Gaussian Model Random Random process
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
B
Mixed random variables problem
I got (a) and (b) but I'm still working on (c). The solutions can be found here for your reference: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-041sc-probabilistic-systems-analysis-and-applied-probability-fall-2013/unit-ii/lecture-9/MIT6_041SCF13_assn05_sol.pdf. But...- baseballfan_ny
- Thread
- Bayes rule Mixed Probability theory Random Random variables Variables
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
A
Graduate Trend in an approximately exponentially distributed random variable
I have a series of variables X i where ultimately the variables Xi each follow approximately an exponential distribution with a constant rate. In the beginning, there is a certain long-term trend. Is there a probability model in which Xi depends on the outcome of Xi-1 so that in the long run...- Ad VanderVen
- Thread
- Distributed Random Random variable Variable
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
S
Prob/Stats Material on complex random variables and exotic probabilities
I am looking for books that have sections or even chapters devoted to complex random variables, or random variables that can take on complex values (NOT probabilities that are valued in the complex range, in this regard). On the other hand, if someone does know any books that contain material on...- s00mb
- Thread
- Complex Material Probabilities Random Random variables Variables
- Replies: 1
- Forum: Science and Math Textbooks
-
S
Undergrad Stratified sampling based on properties of random number streams
I recall seeing briefing notes dating from about the 1970's that advocated doing stratified sampling of the outputs of simulations by using strata based on properties of the random number streams. However, I don't recall how the strata were to be defined. Is this type of stratified sampling a...- Stephen Tashi
- Thread
- Properties Random Random number Sampling
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
M
MHB How Can a Random Number Table Be Used to Sample Cotton-Top Tamarins?
okay guys this is the question: A zoo has 80 cotton-top tamarins. Describe in detail how the random- number table given below could be used to select a sample of 5 of them, for a study of tail lengths. 8330 3992 1840 0330 1290 3237 9165 4815 0766 (5marks) So I am not really sure where to go...- MysticGarC
- Thread
- Random Sampling
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-

Boundary value problem- Random Walker
I want to solve this using difference equation. So I set up the general equation to be Pi = 0.5 Pi+1 + 0.5 i-1 I changed it to euler's form pi = z 0.5z2-z+0.5 = 0 z = 1 since z is a repeated real root I set up general formula Pn = A(1)n+B(1)n then P0 = A = 1 PN = A+BN = 0 -> A= -BN...- potatocake
- Thread
- Boundary Boundary value problem Difference equation Random Value
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

Proof of a formula with two geometric random variables
The image above is the problem and the image below is the solution I have tried but failed.- Armine
- Thread
- Formula Geometric Probability Proof Random Random variable Random variables Variables
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

Concept of Hidrostatic Pressure in Random Shaped Vessel
Hello Everyone! this question is using Indonesian language, i have translated the question at "Homework Statement". The container is filled by water (in Indonesian, "Air" means "Water") i know the the pressure at point X, Y and Z depends on their corresponding depth. my best answer is : Pz >...- Vermilion X
- Thread
- Concept Depth Pressure Random Vessel
- Replies: 2
- Forum: Introductory Physics Homework Help
-

Random Seed Choice for LAMMPS Molecular Dynamics Simulations
I want to create multiple molecular dynamics simulations using LAMMPS which are different only in the initial velocity of the atoms. LAMMPS allows you to use a random seed to generate an initial velocity. I plan to just use successive numbers, so if there are 5 simulations, the seeds would be...- person123
- Thread
- Choice Molecular dynamics Random Random number Seed
- Replies: 21
- Forum: Programming and Computer Science
-

Average of 3 normally distributed random samples
I've found part (i) by calculating the z-score for 40 $$Z = \frac {40- 50} {15} = -0.67$$ $$N(-0.67) = 1- N(0.67) $$ $$1- N(0.67) = 1-0.7486 = 0.2514$$ But parts (ii) and (iii) are confusing me. I have answers provided by my professor that say the mean and std deviation for (ii) and (iii) are...- TheBigDig
- Thread
- Average Distributed Random
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
G
Fortran Solving Magnetic Field Using Floating Random Walk
Hi everyone, I am working on the Fortran code to solve a magnetic field by using "Floating Random Walk" method. I use a square domain for this case and show in the attachment. The external magnetic strength comes from left to right boundary. Both top and bottom are assuming as insulation...- gt24
- Thread
- Floating Random Random walk
- Replies: 6
- Forum: Programming and Computer Science
-
U
MHB Verifying Solution for Exponentially Distributed Random Vars.
Given two i.i.d. random variables $X,Y$, such that $X\sim \exp(1), Y \sim \exp(1)$. I am looking for the probability $\Phi$. However, the analytical solution that I have got does not match with my simulation. I am presenting it here with the hope that someone with rectifies my mistake. ...- user_01
- Thread
- Distributed Random Random variables Variables
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-

High School Adding random noise to a gradient
I am designing the pattern of a quilt my wife is making. The quilt is made of 15x20 squares of exactly six shades of blue - dark at one end to light at the other end. The gradient will be "noisy". I want to experiment with that noise. I am exploring Photoshop to do this visually, but it...- DaveC426913
- Thread
- Gradient Noise Random
- Replies: 22
- Forum: General Math
-

How to Fly a B-26: Official Training Film
How to fly a B-26 - an official training film. Just in case you're ever trapped on a desert island with no means of escape except a B-26...- Ivan Seeking
- Thread
- Random Videos
- Replies: 8
- Forum: General Engineering
-

Generating Random Numbers with the Acceptance-Rejection Method
I'm trying to write a C++ program to generate random numbers using the acceptance-rejection method. To plot the graphs, I'm using ROOT by CERN. I am checking if y values taken from the rectangular boundary are less than or equal to the function ##f(x_{i}) = e^{-k(x_{i} - x_{0})^{2}}##. void...- Amrator
- Thread
- Method Numbers Random
- Replies: 22
- Forum: Programming and Computer Science
-
F
Total movement of bacteria assuming a random distribution
Hello, I have to find an expression for the total movement of a bacteria ##s##, knowing that the bacteria is placed (centered) on a two side ruler at position ##x=0## (so a negative ##x## value means the bacteria has moved to the left of the ruler) and that the probability it moves to ##x## is...- fatpotato
- Thread
- Bacteria Distribution Gaussian Movement Random Random distribution
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Linear combination of random variables
a) Total weight ##W=W_1+W_2+...+W_{25}##.$$E[W]=E[W_1]+E[W_2]+...+E[W_{25}]=25\times76=1900\,kg$$$$\sigma_W=\sqrt{V(W_1)+V(W_2)+...+V(W_{25})}=\sqrt{25\times(16)^2}=80\,kg$$ b) Since ##W## is a linear combination of normal distributions, the reproductive property tells us that ##W## is also...- archaic
- Thread
- Combination Linear Random Random variables Variables
- Replies: 8
- Forum: Precalculus Mathematics Homework Help
-
A
Comp Sci How to Generate Random Numbers in C++ Using `<random>`?
I want to generate random numbers in C++. I do not want to use C library function (`<cstdlib> <ctime> (time.h)` ) and class. So I cannot use `rand()` function in C. I want to generate random integer numbers and I guess I can use `<random>` library in C++11. How can I use this generate random...- anonim
- Thread
- C++ Numbers Random
- Replies: 4
- Forum: Engineering and Comp Sci Homework Help
-
M
Undergrad Failure rate for a uniformly distributed variable
Hi, I have this question: If random variable T is uniformly distributed over [a, b] , what is its failure rate? Please help- Mark J.
- Thread
- Distributed Distribution Failure Random Rate Uniform Variable
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
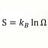
Random Photos
A topic for random photos: Ko-Larn island 7 km West of Pattaya- Point Conception
- Thread
- Photos Random
- Replies: 3,507
- Forum: Fun, Photos and Games
-

Sum of the Expected Values of Two Discrete Random Variables
Apologies if this isn't the right forum for this. In my stats homework we have to prove that the expected value of aX and bY is aE[X]+bE[Y] where X and Y are random variables and a and b are constants. I have come across this proof but I'm a little rusty with summations. How is the jump from the...- TheBigDig
- Thread
- Discrete Expectation value Random Random variables Statistic Sum Variables
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Is Random Mutation Totally "Random" In Biology/Evolution?
When I see the term random mutation in popular writings on evolution (social sciences major here, so please forgive my ignorance), I wonder what it precisely refers to. I understand we can have have gene mutations due to exogenous factors, such as exposure to UV light, or from "errors" in the...- kyphysics
- Thread
- Mutation Random
- Replies: 18
- Forum: Biology and Medical
-
G
Undergrad Question pertaining to the random distribution of many worlds
Hi everyone, I was having a conversation with my friend about the many worlds interpretation of quantum mechanics, and we couldn't figure out if many worlds implied every single last possible conceivable outcome, or if there were certain limitations that the system was confined to. For...- g564321
- Thread
- Distribution Many worlds Random Random distribution
- Replies: 12
- Forum: Quantum Interpretations and Foundations
-

Calculating a mean related to a continuous random variable
I am not sure about how to approach this. Since the volume is uniformly distributed, the mean volume is ##(5.7+5.1)/2=5.4##, which is less than ##5.5##. From this, I could say that, on average, the producer won't spend any extra dollars. But then I thought that maybe I should interpret this as...- archaic
- Thread
- Continuous Mean Random Random variable Variable
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-

Undergrad Is there anything in physics that’s random?
Is there anything in particle or energy physics that is random? If yes why wouldn’t random effects destroy past information? I am asking in relation to the theory that no information is ever lost. If I understand it correctly, I’m not a physicist.- Whipley Snidelash
- Thread
- Physics Random
- Replies: 26
- Forum: High Energy, Nuclear, Particle Physics
-
D
Three independent random variables having Normal distribution
Let ##X_1 X_2 X_3 ## be three independent random variables having Normal(Gaussian ) distribution, all with mean ##\mu##=20 and variance ##\sigma^2##=9. Also let ##S=X_1+ X_2 +X_3## and let ##N## be the number of the ##X_i## assuming values greater than 25. ##E\left[N\right]##=? I did not...- DottZakapa
- Thread
- Distribution Independent Normal Normal distribution Random Random variables Variables
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
D
Two Poisson distributed random variables
How do I evaluate P(X-Y=0)=?- DottZakapa
- Thread
- Distributed Poisson Random Random variables Variables
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
D
Expected value of two uniformly distributed random variables
##X_1## and## X_2## are uniformly distributed random variables with parameters ##(0,1)## then: ##E \left[ min \left\{ X_1 , X_2 \right\} \right] = ## what should I do with that min?- DottZakapa
- Thread
- Distributed Expected value Random Random variables Value Variables
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Graduate Is randomness real or the inability to perceive hyper complex order?
How did you find PF?: random Brownian motion Is randomness real or is it simply defined as such due to our inability to perceive hyper complex order? Randomness is a troublesome word. I'd feel better if I knew it was an objective phenomenon and not merely a placeholder description of...- blazh femur
- Thread
- Complex Entropy Random Randomness
- Replies: 16
- Forum: Quantum Physics
-
D
Uniform distribution of two random variables
i did not get how the professor came to such result. In particular: in order to evaluate P[x+y<=z] solved a double integral of the joint density. What i am not getting is did i choose the extreme of integration in order to get as result ##\frac {z^2} {2}##- DottZakapa
- Thread
- Distribution Random Random variables Uniform Uniform distribution Variables
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
Undergrad Quantum Spin: Is it Random? Alice & Bob's Test
I got confronted with this issue: Suppose we have Alice and Bob, each of them measuring the quantum spin on one of a pair of electrons along parallel axes, thus yielding an identical spin for both with each measurement. Now Alice's measurement is done earlier than Bob's. Can we now predict...- entropy1
- Thread
- Random Spin
- Replies: 38
- Forum: Quantum Physics
-
F
Understanding the PMF of a Random Variable: A Brief Overview
I am new to the topic so I do need your help here. Thanks in advance- flughafen
- Thread
- Random Random variable Variable
- Replies: 4
- Forum: Introductory Physics Homework Help
-

Calculating the Probability of Two Men Meeting Again with a Double Random Walk
I set up the problem in the following way: considering the relative motion, at each step there is a probability that - they take a step in the opposite direction going away from each other, so the distance increases and the associated probability is 1/4 - they take a step in the opposite...- dRic2
- Thread
- Random Random walk
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
E
High School How do we interpret a random variable?
I've read that we can define a random variable on a probability space ##(\Omega, F, P)## such that it is a function that maps elements of the sample space to a measurable space - for instance, the reals - i.e. ##X: \Omega \rightarrow \mathbb{R}##. That being said, it's often treated (at least...- etotheipi
- Thread
- Random Random variable Variable
- Replies: 10
- Forum: Set Theory, Logic, Probability, Statistics
-
J
MHB Minimum Degree of a Random Graph (Probabilistic Method)
Problem: Suppose that the function $p : N \rightarrow [0, 1]$ satisfies $p >> n^{-1}ln(n)$ (i.e. $n^{-1}ln(n) = o(p)$). (a) Prove that as $n \rightarrow \infty$, the random graph $G(n, p)$ has minimum degree at least $\frac{np}{2}$ almost surely. Idea: Look at the degree of each individual...- joypav
- Thread
- Degree Graph Method Minimum Random
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
High School Random lengths of Collatz chains
Assuming its hail stone series is pseudo-random, the Collatz algorithm divides by 2 twice for each multiplication by 3. This means that for every three iterations the test value is on average reduced by 1/4, or 1/12 per iteration. I've tweaked the algorithm to produce much longer series for...- Chris Miller
- Thread
- Random
- Replies: 14
- Forum: Set Theory, Logic, Probability, Statistics
-
J
MHB Are Events in Random Graphs from G(n, 1/2) Independent?
Let $n$ be a positive integer, and let $G$ be a random graph from $G(n, 1/2)$. Let $e_1, . . . , e_{n \choose 2}$ be the possible edges on the vertex set ${1, . . . , n}$, and for each $i$, let $A_i$ be the event that $e_i ∈ E(G)$. Prove that the events $A_1, . . . , A_{n \choose 2}$ are...- joypav
- Thread
- Graph Random
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-

Graduate Langevin equation - derivative of random force?
Greetings, I am struggling with an exercise to the Langevin equation. Suppose we are given the following differential equation for a particle's 1D time-dependent momentum ##p(t)##: $$\text{d}p = -\gamma p \text{d}t + F(r)\text{d}t + \sqrt{C\gamma}\text{d}W $$ with a constant ##C##, a...- SchroedingersLion
- Thread
- Derivative Force Random
- Replies: 8
- Forum: Quantum Physics
-
A
Graduate Third and fourth central moment of a random variable
My question is as follows. In the attached paper a formula is given on page 272 for the expectation of Tn (formula 23) and for the variance of Tn (formula 24). Now I would like to know what the formulas look like for Tn 's third and fourth central moment.- Ad VanderVen
- Thread
- Moment Random Random variable Variable
- Replies: 12
- Forum: Set Theory, Logic, Probability, Statistics
-
L
Comp Sci How Does C++ Handle Random Number Generation in Coin Toss Simulations?
The program works as intended. #include <iostream> #include <ctime> #include <cstdlib> int coinToss ();int main () { int tosses, result; std::count << "How many coin tosses? "; std::cin >> tosses; size_t seeder = time(0); srand(seeder); for (int i = 0; i < tosses...- Lord Anoobis
- Thread
- C++ Generation Random Random number
- Replies: 10
- Forum: Engineering and Comp Sci Homework Help
-
F
Undergrad Distribution of a sample random variable
$X_1, X_2, ..., X_{15}$ are independently to each other and follow $N (7, 3^2)$ what distribution the following statistics follow$T = \frac{(\bar{X}− 7)}{\sqrt{s^2/15}}$i know this follow t distribution $t_(n-1) =t_{14}$but how do i find what distribution $T^2$ follows, can i just multiply it?$T...- fiksx
- Thread
- Distribution Random Random variable Variable
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics