2 exercises on changing variables of double integrals

[carlosbgois]

Homework Statement

a) $\int\int_{B}\frac{\sqrt[3]{y-x}}{1+y+x} dxdy$, where B is the triangle with vertices $(0, 0), (1, 0), (0, 1)$.

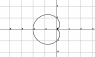
b)$\int\int_{B}x dxdy$ where B is the set, in the xy plane, limited by the cardioid $ρ=1-cos(θ)$

The Attempt at a Solution

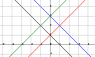
a) Let $ψ: \left\{u = y-x, v = 1+y+x\right\}$. Then ψ has an inverse of class $C^{1}$, and the jacobian of this transform is $\frac{-1}{2}$, and also B is limited by $x=0, y=0, y=-x+1$, which over the ψ transform becomes, respectively $v=u+1, v=-u-1, v=2$. For last, by drawing perpendicular u and v axis and limiting the region, I could see that the first two transforms intercept and $v=0$. Then I did $\frac{-1}{2}\int^{2}_{1}\left[\int^{v-1}_{1-v}\frac{\sqrt[3]{u}}{v} du\right]dv$.

and I don't think this is going anywhere because most values of u inside the transformed B are negative, and the solution will have a complex part, which I'm sure it shouldn't.

b) (this attempt has a mistake, see edit below)As the cardiod is is polar coordinates, we may change x to those coordinates too, hence $x=ρcos(θ)$. As the image of the cosine is $[-1, 1]$, then $0≤ρ≤2$, and I also made $0≤θ≤2\pi$, hence the integral becomes $\int^{2\pi}_{0}\left[cos(θ)\int^{2}_{0}ρ^{2} dρ\right] dθ$.

By solving this I got 0, and I don't think it's correct.

[EDIT]
b) I found one mistakes in letter b: the interval for ρ is not as said before, it is $0≤ρ≤1-cos(θ)$, hence the 'correct' integral is $\frac{1}{3}\int^{2\pi}_{0}cos(θ) (1-cos(θ))^{3} dθ.$

For solving this I have expanded the integrand and determined the first two terms using integration by parts, and the other two were direct. My result is $\frac{-5\pi}{4}$.

New questions: Is the result correct? Is there any faster way to integrate the expression, instead of expandind and evaluating term by term?

Thanks

 

[clamtrox]

Are you sure you got the vertices right in a)? That triangle indeed has half of it in the region where y<x, meaning you get a complex solution.

The answer to b) looks fine; you could try substituting 1-cos(theta) = sin(t) to make the integral slightly easier.

 

[carlosbgois]

Thanks. I rechecked and the vertices are correct (according to the book). It gives a hint: make u=y-x, and v=1+y+x, which I did, but there`s no answer to the problem.

 

[DryRun]

Using $u=y-x$ and $v=1+y+x$, find the Jacobian:
$$J=\frac{\partial (u,v)}{\partial (x,y)}$$

 

[clamtrox]

If you want, you could try doing it with vertices (0,0), (0,1) and (1,1) instead. But the way that problem is given, it's clear that the solution should be complex unless there are some weird cancellations.

 

[DryRun]

For part (a), you should get:
$$\int^3_2 \int^{(3-v)}_{(v-3)} \frac{\sqrt[3]u}{v}\,.dudv$$
Or
$$\int^2_1 \int^{(v-1)}_{(1-v)} \frac{\sqrt[3]u}{v}\,.dudv$$
I have attached the graph of the triangle in the u-v plane.

 

[DryRun]

For part (b), you should get:
$$\int^{2\pi}_0 \int^{1-\cos \theta}_0 (\rho^2-\rho^3) \,.d\rho d\theta$$
See the attached graph.