masterchiefo
- 211
- 2
Homework Statement
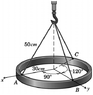
metal piece = 300N
As this metal piece is in balance, what is the tension in each cable?
Picture of the problem in attachment.
Homework Equations
The Attempt at a Solution
W = 300*[0 0 1]D to A:
vtda = tda [sin(37), sin(37)*sin(90), -cos(37)]
D to B:
vtdb = tdb [sin(37)*sin(90), sin(37), - cos(37)]
D to C
vtdc = tdc [cos(30)*sin(37), -sin(30)*sin(37), -cos(37)]
solve([0 0 0]=300*[0 0 1])+vtda+vtdb+vtdb, {tda,tdb,tdc}
I have been trying to find the mistake for 3 hours but I really can't find it :/
When I solve with my TI calculator I get a "false"
thank you very much