A box on a moving wedge, on an inclined plane

[Demon117]

Homework Statement

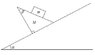
The situation is indicated in the diagram below. Block m is at rest, and the block M has an initial velocity upward. Need to find the Lagrangian of this system, and then the Euler-Lagrange equations.

The Attempt at a Solution

This is the Lagrange that I came up with from the beginning, but it seems like I am oversimplifying it:

$T=(1/2)m(\dot{x_{1}}^{2}+\dot{y_{1}}^{2})+(1/2)M(\dot{x_{2}}^{2}+\dot{y_{2}}^{2})$

$V= mgy_{1}cos(\beta) + Mgy_{2}cos(\alpha)$

$L=(1/2)m(\dot{x_{1}}^{2}+\dot{y_{1}}^{2})+(1/2)M(\dot{x_{2}}^{2}+\dot{y_{2}}^{2}) - mgy_{1}cos(\beta) - Mgy_{2}cos(\alpha)$

Like I said, this seems over simplified and I feel like there should be some cross terms in the kinetic energies. The second attempt that I have made is try to come up with velocity vectors. In this case I have the velocity of the wedge with respect to the incline $v_{w}=\left(\partial _tx_2\right)\hat{i}-\left(\partial _ty_2\right)\hat{j}$ and the velocity of the box with respect to the wedge, with respect to the incline $v_{B}=\left(\partial _tx_2\right)\hat{i}-\left(\partial _ty_2\right)\hat{j}+\left(\partial _tx_1\right)\hat{i}'-\left(\partial _ty_1\right)\hat{j}'$.


Geometry has always been an extreme weakness of mine. It seems like I am approaching this in all of the wrong ways. Any suggestions would be helpful.

 

[dikmikkel]

You have to write your generalized coordinates at first, then you would have some cos sine dependence in the velocity. That is because the box is constrained to move in a certain way and by not introducing gen. coordinates you would simply get Newtons 2nd law.
Also your potential energies have different zero points?
Define a coordinate system