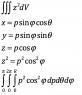Am I setting this integral up correctly?

[SarahAlbert]

Homework Statement

Use spherical coordinates to evaluate the integral over a sphere of radius R.

Homework Equations

The equation of my sphere would be x^2+y^2+z^2=R^2
Please see the attached file.

The Attempt at a Solution

I have attached a file to show my work so far. Evaluating the integral once it is set up should be fine, I'm concerned it's not set up correctly. Thank you.

 

[BvU]

Hello,
You want to reconsider dV. $\ \ \ dV \ne dr\, d\phi \,d\theta$.

 

[SarahAlbert]

I'm beginning to think that it's also not as easy as (pcos∂)^2 since my radius is R then p=R so isn't it ∫∫∫pcos∂)^2p^2

 

[PWiz]

I'm beginning to think that it's also not as easy as (pcos∂)^2 since my radius is R then p=R so isn't it ∫∫∫pcos∂)^2p^2

Nope. You're integrating p over a radius of R. It's not the same thing.

 

[BvU]

You are calculating a volume integral, so your p is running from 0 to R .

Your function to integrate is $\ f(r, \theta, \phi) = (r\cos\theta)^2$ as you wrote correctly.

Now check out how you can express a volume element in spherical coordinates $dV(r, \theta, \phi)$ , e.g. as shown here or here

 

[SarahAlbert]

You are calculating a volume integral, so your p is running from 0 to R .

Your function to integrate is $\ f(r, \theta, \phi) = (r\cos\theta)^2$ as you wrote correctly.

Now check out how you can express a volume element in spherical coordinates $dV(r, \theta, \phi)$ , e.g. as shown here or here

So it would then be (rcosθ)^2r^2sinθdrdθdphi which becomes r^2sinθcosθdrdθdphi and then become r^2sin(2θ)/2drdθdphi