Matt Chu
- 16
- 0
Homework Statement
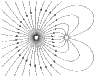
Two charges 2q and -q are located at x = 0 and x = a respectively. There are field lines extending from the positive charge and lines going inwards to the negative charge. Some of these lines go from the positive charge to the negative, but some go off to infinity from the positive charge. The question asks to find the angle at which the lines go towards infinity. (It also mentions to use a "cleverly chosen Gaussian surface.)
Homework Equations
Gauss's law
∫ E⋅dA = qen/ε0
The Attempt at a Solution
I tried to maybe using Gauss's law on the two charges individually, then on both charges together. I'm not sure exactly what a "cleverly chosen Gaussian surface" is, so I don't know exactly how to proceed.