I Angle of repose - Trying to understand the formula

[k.udhay]

I recently posted a question on similar line and got few good explanations as well. Still, I am unable to understand clearly. Hence I am going more specific this time.

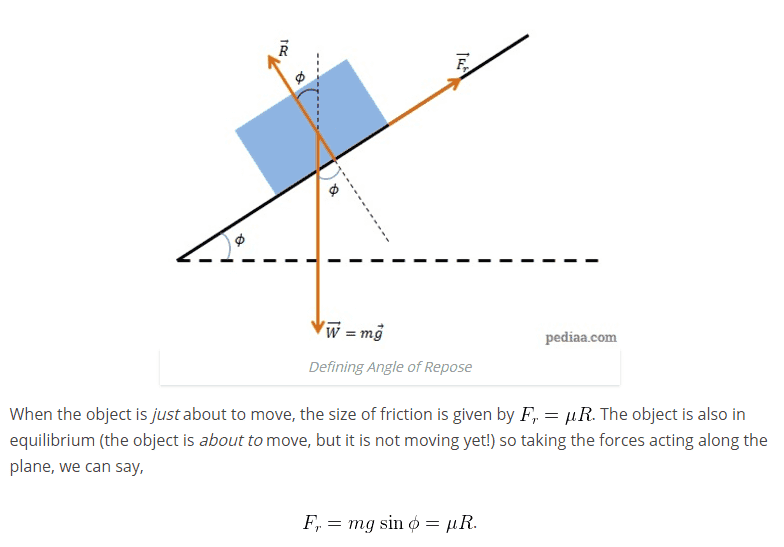
In the given picture taken from internet, friction force acting between an inclined plane and an object is defined as F_r = W x sin (phi).

Does it mean the friction force (acting upwards!) increases with slope of the gradient? In practice, the object starts falling down as the slope increases. That should mean that the friction force reduces with slope, shouldn't it? I feel the formula and actual are contradicting. Though, I am sure I am mistaken somewhere. Pl. help. Thanks.

@haruspex @mike.Albert99 @sophiecentaur

 

[BvU]

Let's try to be precise, then:

In the given picture taken from internet, friction force acting between an inclined plane and an object is defined as Fr = W x sin (phi)

Should be:
friction force acting between an inclined plane and an object that does not slide is calculated to be as Fr = W x sin (phi)

Does it mean the friction force (acting upwards!) increases with slope of the gradient?

That is correct. $\ \phi = 0 \ \Rightarrow \ F_{\rm friction} = 0$
You can see it from Fr = W x sin (phi) as well.

That should mean that the friction force reduces with slope, shouldn't it?

No. Gravity is pulling downwards along the plane with a force $mg\;\sin\phi$. As long as the block doesn't start sliding, this downward pulling component of gravity is offset by the friction force, which is acting in an upward direction along the slope.

If you gradually increase the angle, there comes a moment when the maximum friction force $\mu \;mg\;{\bf \cos} \phi$ is reached and for any $\phi$ above that the block will slide.

At this maximum $\phi$ you can write $\mu \;mg\;{\bf \cos} \phi + (-\;mg\; \sin \phi ) = 0 \ \Rightarrow \ \mu = \tan\phi_{\rm max}\$

With the minus sign I indicate the force is acting in a direction opposite the $\mu \;mg\;{\bf \cos} \phi$, i.e. I choose downward along the plane as positive.

[edit] Sorry -- someone should have corrected this:
With the minus sign I indicate the force $\;mg\; \sin \phi\$ from gravity is acting in a direction opposite the force $\mu \;mg\;{\bf \cos} \phi$ from friction, i.e. I choose upward along the plane as positive, and I take the numerical value of $g$ as positive.

 

[Cutter Ketch]

To expand now with less precision, yes the force of friction changes with the applied forces to prevent motion right up to the point that the required force exceeds the maximum possible force as indicated by the coefficient of static friction. At that point the box slips and the force of friction drops to the "constant" value of sliding friction. (Constant in quotes because real surfaces are irregular and the force of sliding friction will vary as the conditions vary while sliding.). So sliding friction is a force of a fixed magnitude (in fixed conditions), but static friction is a force of constraint (there's a correct term, but I can't think of it) taking on any value necessary to oppose motion (up to a maximum). So is the normal force in this problem, by the way.

 

[haruspex]

To expand now with less precision, yes the force of friction changes with the applied forces to prevent motion right up to the point that the required force exceeds the maximum possible force as indicated by the coefficient of static friction. At that point the box slips and the force of friction drops to the "constant" value of sliding friction. (Constant in quotes because real surfaces are irregular and the force of sliding friction will vary as the conditions vary while sliding.). So sliding friction is a force of a fixed magnitude (in fixed conditions), but static friction is a force of constraint (there's a correct term, but I can't think of it) taking on any value necessary to oppose motion (up to a maximum). So is the normal force in this problem, by the way.

That's all good.