Est120
- 54
- 3
- Homework Statement
- write the macroscopic angular momentum balance for the following problem
- Relevant Equations
- see image
we neglect gravity and viscosity efects
i really can't understand how does the author managed to get the equation in the image
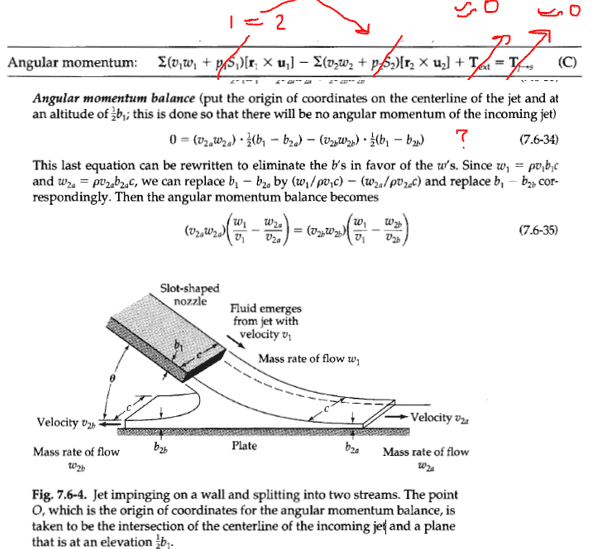
i really can't understand how does the author managed to get the equation in the image