Joshua A
- 10
- 0
Homework Statement
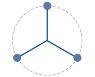
Three small, identical 0.70-kg pucks are attached to identical 0.50-m strings, tied together at a common center as shown in (Figure 1) . Pucks are whirled in circular motion at angular speed 3.0 s-1
What is the magnitude of the angular momentum of the system about the common center?
Homework Equations
I = mr2
Lθ = Iwθ
The Attempt at a Solution
Angular momentum is a vector, therefore the angular momentum of this system should be 0 kg m2/s as all the vectors will cancel out. The magnitude of that is also 0 kg m2/s.
Apparently this answer is wrong. Where am I going wrong? When they ask for the magnitude of the angular momentum, do they want me to find the magnitude of the angular momentum for each puck and then add the magnitudes together?