garr6120
- 42
- 0
Members are reminded to use the 3 header template in the homework help forums
Given the circuit in the diagram I was wondering would I be able to make ib equal to the mesh i3.
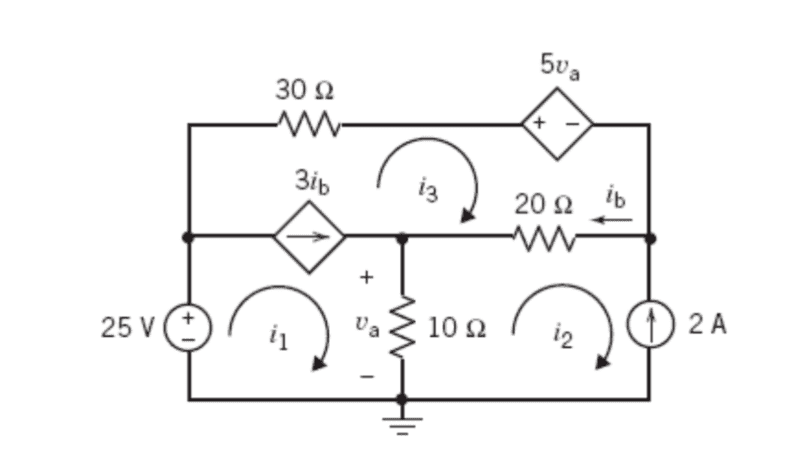
I have the equation for my Super Mesh at i1 and i3 which is:
-25+30i3+5Va+20(i3-i2)+10(i1-i2)=0 (1).
The mesh i2 is equal to -2A (2).
subbing (2) into (1) gives:
-25+50i3+5Va-30i2+10i1=0 (3).
Va=i1-i2 (4).
subbing (4) into (3) gives: -25+50i3-35i2+15i1=0 (5).
subbing (2) into (5).
45+50i3+15i1=0 (6).
3ib=i1-i3 (7).
Now I almost have one unknown. Is it possible to set ib equal to i3 so i can isolate for i1 in equation 7. If i can't how would i be able to solve it.
Also, are the steps to finding the mesh currents correct for this problem?
I have the equation for my Super Mesh at i1 and i3 which is:
-25+30i3+5Va+20(i3-i2)+10(i1-i2)=0 (1).
The mesh i2 is equal to -2A (2).
subbing (2) into (1) gives:
-25+50i3+5Va-30i2+10i1=0 (3).
Va=i1-i2 (4).
subbing (4) into (3) gives: -25+50i3-35i2+15i1=0 (5).
subbing (2) into (5).
45+50i3+15i1=0 (6).
3ib=i1-i3 (7).
Now I almost have one unknown. Is it possible to set ib equal to i3 so i can isolate for i1 in equation 7. If i can't how would i be able to solve it.
Also, are the steps to finding the mesh currents correct for this problem?

