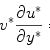You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Are PEDs Impacting Amateur Sports Integrity?
- Thread starter thepioneerm
- Start date
Physics news on Phys.org
coomast
- 279
- 1
I had a look at it and after a few minutes I got a transformed result, but indeed it is not the one given. However there seems to be a term missing in the left hand side containing the time t. After using the transformation I got (without the term with the time):
u^*\frac{\partial u^*}{\partial x^*}+ v^*\frac{\partial u^*}{\partial y^*}= m\cdot \frac{U^{n-1}}{L^n}\cdot \left[M\cdot \theta + \frac{\partial}{\partial y^*} \left[\left|\frac{\partial u^*}{\partial y^*}\right| ^{n-1} \right]\cdot \frac{\partial u^*}{\partial y^*}\right]
Maybe the term with t can shed some light on the necessary next step, otherwise I do not see how to reach the end result.
coomast
u^*\frac{\partial u^*}{\partial x^*}+ v^*\frac{\partial u^*}{\partial y^*}= m\cdot \frac{U^{n-1}}{L^n}\cdot \left[M\cdot \theta + \frac{\partial}{\partial y^*} \left[\left|\frac{\partial u^*}{\partial y^*}\right| ^{n-1} \right]\cdot \frac{\partial u^*}{\partial y^*}\right]
Maybe the term with t can shed some light on the necessary next step, otherwise I do not see how to reach the end result.
coomast
coomast
- 279
- 1
thepioneerm said:coomast
thank you very much
but how do you reach this result ??!
please can you explain it to me
even I don't know how to get
pfff...the preview gives a different formula then the one I'm typing, I assume the latex is still broken
This is done in the same way as before, you have:
v\frac{\partial u}{\partial y}=v^*U\frac{\partial u^*U}{\partial y^*L} = \frac{U^2}{L} v^*\frac{\partial u^*}{\partial y^*}
After doing this to the other terms as well, you end up with the result I gave earlier. Beware of the error in the question, you will not be able to reach the solution given.
remark 1: sorry for the late reply, I had a busy week
remark 2: don't use a font this big, it looks as if you are shouting which is not the intention I suppose, instead look at learning the basics of latex, it will be helpfull in producing the nice formula's out here :-) [if the bloody thing works, lol]
seems the latex is OK after all... this does not follow a mathematical rule, perhaps something chaotic...could be me as well...
best regards,
coomast
thepioneerm
- 33
- 0
coomast
thank thank thank you very very very much
and I will not use a font this big ^-^
and I will try to learn the basics of latex
thank you
thank thank thank you very very very much
and I will not use a font this big ^-^
and I will try to learn the basics of latex
thank you
Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$
Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$
The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$
Plugging identity above into ##(1)## with ##u...
Similar threads
- Replies
- 20
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 6
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 17
- Views
- 5K
- Replies
- 3
- Views
- 3K
- Replies
- 8
- Views
- 1K
- Replies
- 2
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
-
Finding the modulus and argument of ##\dfrac{a}{(b±ci)^n}##
- Started by chwala
- Replies: 17
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 10
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math