bananabandana
- 112
- 5
Homework Statement
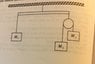
Please see attached for diagram. We know that the elevator arm is horizontal when the lift is stationary, with ## M_{1}=\frac{4M_{2}M_{3}}{(M_{2}+M_{3})}## It wants us to find out if this is still the case when the lift is accelerated upwards at a constant velocity ##g##
Homework Equations
The Attempt at a Solution
Let the tension in the ##M_{1}## rope be ##T_{1}##, that in the rope between the lift and the support for ##M_{2}## and ##M_{3}## be ##T_{A}## and that in the rope between masses ##M_{2}## and ##M_{3}## be ##T_{B}## Take up as positive (i.e lift is moving up at ## +g##) [/B]
Look at ##M_{1}## first:
$$ T_{1}-M_{1}g=M_{1}g \implies T_{1}=2M_{1}g $$
Then look at the ##M_{2},M_{3}## system to work out ##T_{B}##:
$$ T_{B}-M_{2}g=M_{2}(g+a) $$
$$ T_{B}-M_{3}g=M_{3}(g-a) $$
Substitute for ## T_{B}## and rearrange for ## a##:
$$ a = \frac{M_{3}-M_{2}}{M_{3}+M_{2}}g $$
$$ T_{B} = 2M_{2}g+M_{2}a = \frac{4M_{3}M_{2}g}{(M_{3}+M_{2}} $$
Therefore:
$$ T_{A} = 2\times T_{B} = \frac{8M_{3}M_{2}g}{(M_{3}+M_{2})} $$
So the thing is stable when accelerating cosntantly as the torque to ##T_{1}## is balanced by that due to ##T_{A}##, from our relationship for ##M_{1}##.
But I have two questions - one is there not some easier (intuitive way) to think about the motion of the system in the accelerating frame that I wasn't smart enough to find? - and two - when I first did the problem I wrote down:
$$ T_{A}-2T_{B} = (M_{2}+M_{3})g $$ - I figure this is false because there is no mass in the rope, so that even if it is accelerating with speed ##g## then we don't need to worry about ##M_{2}## and ##M_{3}## as they are already taken care of by the tension?
Thanks!