You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
AI Thread Summary
The discussion revolves around the axial loading of a composite beam, focusing on the calculations of compressive forces and stresses in brass and steel components. A key point is the need to correctly account for the compressive force applied to the brass section, which is influenced by the yield stress of the materials involved. The participants clarify the arithmetic involved in determining the forces and stresses, emphasizing the importance of understanding the bi-directional nature of tension and compression. The conversation highlights the necessity of confirming calculations to ensure accuracy in solving axial load problems. Overall, the dialogue underscores the complexities of axial loading in composite materials and the critical nature of precise calculations in engineering.
Physics news on Phys.org
ski0331
- 10
- 0
Basically I'm asking if I did this correctly and have the correct answer and if I don't, what I did wrong and where I went wrong in my thinking.
- 23,706
- 5,921
I confirm the result in the first part, but I don't follow what you did in the 2nd part. It seems to me for the 2nd part, all you need to do is add a compressive force to the entire rod that compresses it 13.04 mm: $$\frac{FL_1}{A_1E_1}+\frac{FL_2}{A_2E_2}=-0.01304$$
ski0331
- 10
- 0
Where did you get the 13.04 mm? And I thought I did add them together f=-ax and f2=-ax+4000N
- 23,706
- 5,921
I'm just doing it as 2 superimposed problems. In the first part, you showed that the growth of the bar would be 14.04 mm if the bar were totally unconstrained. Since the original gap was 1 mm, that would mean that you would have to compress the bar 13.04 mm to get it to fit into the available space.ski0331 said:Where did you get the 13.04 mm? And I thought I did add them together f=-ax and f2=-ax+4000N
Assuming purely elastic behavior, this gives a compressive stress of 106 MPa in the Brass and a compressive stress of 131 MPa in the steel. But the yield stress of the Brass is only 78 MPa. How do you think that would affect the answer?
Last edited:
ski0331
- 10
- 0
I'm not sure. would it? I've struggled with this subject (axial loads). But a guess would be that it would bend the brass?Chestermiller said:I'm just doing it as 2 superimposed problems. In the first part, you showed that the growth of the bar would be 14.04 mm if the bar were totally unconstrained. Since the original gap was 1 mm, that would mean that you would have to compress the bar 13.04 mm to get it to fit into the available space.
Assuming purely elastic behavior, this gives a compressive stress of 106 MPa in the Brass and a compressive stress of 131 MPa in the steel. But the yield stress of the Brass is only 78 MPa. How do you think that would affect the answer?
- 23,706
- 5,921
When you complete the solution of the purely elastic problem and have confirmed my answer, we can talk about what to do because the compressive yield stress of the brass is reached.ski0331 said:I'm not sure. would it? I've struggled with this subject (axial loads). But a guess would be that it would bend the brass?
Your solution for the elastic problem is incorrect because you included the 4000 with the steel rather than with the brass.
ski0331
- 10
- 0
ahhh ok I see where I did that! That makes sense, but I make my first cut to determine what Ax is for my free body diagram before the 4Kn. Like I said axial loads have been giving me fits to solve.Chestermiller said:When you complete the solution of the purely elastic problem and have confirmed my answer, we can talk about what to do because the compressive yield stress of the brass is reached.
Your solution for the elastic problem is incorrect because you included the 4000 with the steel rather than with the brass.
- 23,706
- 5,921
OK. Let's see what you get now. It seemed to me you were doing pretty well up to this point.ski0331 said:ahhh ok I see where I did that! That makes sense, but I make my first cut to determine what Ax is for my free body diagram before the 4Kn. Like I said axial loads have been giving me fits to solve.
- 23,706
- 5,921
No. You need to be careful with your arithmetic: $$-\frac{(A_x+4000)(10)}{(101\times 10^9)(100\times 10^{-6})}-\frac{(A_x)(10)}{(200\times 10^9)(50\times 10^{-6})}+0.018=0.001$$ where ##A_x## is a positive compressive force. What do you get for ##A_x##? What do you get for F from my equation in post #3?ski0331 said:
ski0331
- 10
- 0
A(x) I got is equal to 6552.24, F=-6552.44Chestermiller said:No. You need to be careful with your arithmetic: $$-\frac{(A_x+4000)(10)}{(101\times 10^9)(100\times 10^{-6})}-\frac{(A_x)(10)}{(200\times 10^9)(50\times 10^{-6})}+0.018=0.001$$ where ##A_x## is a positive compressive force. What do you get for ##A_x##? What do you get for F from my equation in post #3?
- 23,706
- 5,921
I confirm. I treated F as tension and got a negative number, while you treated it as compression and got a positive number. So this is the compressive force on the steel rod, and the compressive force on the brass rod is 6552+4000=10552 N. What do these solutions to the elastic problem (neglecting the yield stress) give you for the stresses in the brass and the steel?ski0331 said:A(x) I got is equal to 6552.24, F=-6552.44
ski0331
- 10
- 0
Chestermiller said:I confirm. I treated F as tension and got a negative number, while you treated it as compression and got a positive number. So this is the compressive force on the steel rod, and the compressive force on the brass rod is 6552+4000=10552 N. What do these solutions to the elastic problem (neglecting the yield stress) give you for the stresses in the brass and the steel?
Attachments
- 23,706
- 5,921
ski0331 said:
Attachments
ski0331
- 10
- 0
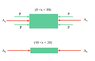
ok you lost me on this chart. why are there 4p? 2 ax?Chestermiller said:
- 23,706
- 5,921
The forces on the left are the reaction forces from the constraint. The 2 P forces on the right are the applied forces. The Ax on the right is the compressive force applied on the brass section by the steel section.ski0331 said:ok you lost me on this chart. why are there 4p? 2 ax?
You are aware that tension and compression are bi-directional, arising from the application of the Cauchy stress relationship to determine the forces acting on a surface? You remember from freshman physics the tension in a rope pointing to the right (for the force the material on the right applies to the material on the left), and to the left (for the force the material on the left applies to the material on the right), correct?
ski0331
- 10
- 0
yes but Ax is the reaction forces of the wall. In my FBD Ax pushes back on 2p and the Normal force.Chestermiller said:The forces on the left are the reaction forces from the constraint. The 2 P forces on the right are the applied forces. The Ax on the right is the compressive force applied on the brass section by the steel section.
You are aware that tension and compression are bi-directional, arising from the application of the Cauchy stress relationship to determine the forces acting on a surface? You remember from freshman physics the tension in a rope pointing to the right (for the force the material on the right applies to the material on the left), and to the left (for the force the material on the left applies to the material on the right), correct?
- 23,706
- 5,921
Taking each section as a free body, the forces on the two ends of each section must be equal in magnitude and opposite in direction. Otherwise, the sections could not each be in force equilibrium.ski0331 said:yes but Ax is the reaction forces of the wall. In my FBD Ax pushes back on 2p and the Normal force.
- 23,706
- 5,921
An overall force balance on the composite beam tells you that the reaction force on the left boundary has to be ##A_x+2P##.
Similar threads
- Replies
- 4
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 3
- Views
- 3K
- Replies
- 3
- Views
- 2K
- Replies
- 8
- Views
- 2K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
-
Engineering Diff gain of a push pull degenerated differential pair
- Started by arhzz
- Replies: 6
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math