Calculate Rotational Inertia of Wheel | 15kg Object on Frictionless Incline

AI Thread Summary
A 15.0-kg object on a frictionless incline is connected to a wheel with a radius of 9.0 cm, and its acceleration is measured at 2.00 m/s². The tension in the rope is calculated to be approximately 58.47 N. The discussion revolves around determining the moment of inertia of the wheel, with participants struggling to apply the correct formulas. The correct formula for calculating the moment of inertia is confirmed as I = Fr²/a. This exchange highlights the importance of using the right equations in rotational dynamics.
ace214
Messages
28
Reaction score
0
A 15.0-kg object is attached to a cord that is wrapped around a wheel of radius r = 9.0 cm (Fig. P8.60). The acceleration of the object down the frictionless incline is measured to be 2.00 m/s2. Assume the axle of the wheel to be frictionless.

p8-60alt.gif


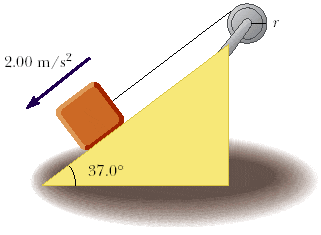
(a) Determine the tension in the rope.
58.46681 N
(b) Determine the moment of inertia of the wheel.
kg·m2
(c) Determine the angular speed of the wheel 2.00 s after it begins rotating, starting from rest.
rad/s
===================================
The tension is correct. I'm stuck on the inertia. I'll use 't' for torque and 'T' for the tension.

t=Iar => I = t/ar = Fr/ar = T/a but this doesn't work. I also tried using the force of gravity and the sigma force in the above equation and none of them are correct.Due tomorrow morning at 8:30 AM EST... :-(
 
Last edited:
Physics news on Phys.org
I guess, the formula is t = Ia/r ... ain't it?
 
saket said:
I guess, the formula is t = Ia/r ... ain't it?
... Crap

Yeah that did it. Thanks.

So for anyone searching the formula becomes
I = Fr^2/a
 
Last edited:

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Question on Moment of Inertia/Rotational Inertia
Replies
4
Views
2K
How Does the Rotational Inertia Affect Rolling Motion on an Inclined Plane?
Replies
3
Views
2K
B Rotational Dynamics: Confused about the tension in this string pulling a mass up an incline
Replies
2
Views
1K
Rotational Motion Two Questions
Replies
12
Views
4K
Calculating Tension, Moment of Inertia, and Angular Speed in a Rotating System
Replies
5
Views
2K
Calculation of torque to stop a wheel.
Replies
4
Views
6K
Moment of inertia of a wheel: linear to angular motion
Replies
6
Views
2K
Inertia block on inclined surface problem? help with solution?
Replies
5
Views
2K
How Do You Calculate the Moment of Inertia for a Rotating Wheel?
Replies
3
Views
2K
Calculating the Force on a Bicycle Wheel
Replies
2
Views
4K

Hot Threads

Recent Insights

Back
Top